Dùng eke vẽ đường thẳng d’ đi qua A vuông góc với đường thẳng d ở hình bên. (Lẽ dĩ nhiên là chỉ vẽ được đường thẳng d’ trên mặt giấy trong phạm vi khung)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


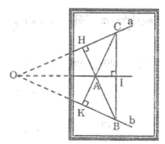
- Kẻ AH ⊥ a kéo dài HA cắt b tại B
- Kẻ AK ⊥ b kéo dài KA cắt a tại C
- Nối BC
- Kẻ AI ⊥ BC, đường thẳng AI đi qua O
Chứng minh:
Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.
Khi đó OA là đường cao thứ ba nên OA ⊥ BC.
Lại có: AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau ( vì qua 1 điểm nằm ngoài 1 đường thẳng ta vẽ được một và chỉ một đường thẳng vuông góc với đường thẳng cho trước).
Suy ra: đường thẳng AI đi qua O.

- Kẻ AH⊥aAH⊥a kéo dài, HA cắt b tại B.
- Kẻ AK⊥bAK⊥b kéo dài KA cắt a tại C.
- Kẻ AI⊥BCAI⊥BC, đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên OA⊥BCOA⊥BC
AI⊥BCAI⊥BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.

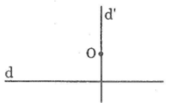
- Đặt êke sao cho một cạnh góc vuông trùng với đường thẳng d.
- Trượt thước theo đường thẳng d đến khi cạnh còn lại đi qua điểm O.
- Kẻ đường thẳng đi qua cạnh góc vuông thứ hai ta được đường thẳng đi qua O và vuông góc với d

-Dùng thước thửng vẽ đg thẳng d
-Lấy điểm O ngoài đg thẳng d
-Đặt eke sao cho 1 cạch của eke trùng với đg thẳng d, cạnh còn lại chứa điểm d
- Vẽ đg thẳng d' chứa điểm O đi qua cạnh của eke
mk có cách dựng đường vuông góc chính xác hơn nhiều mà chỉ dùng thước và compa
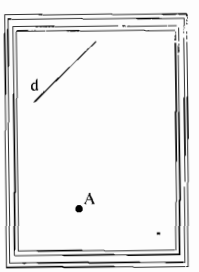
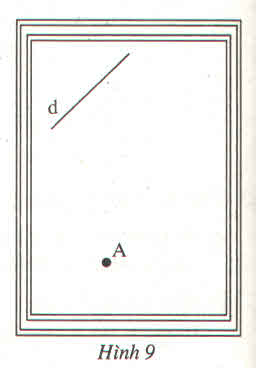


Lấy điểm B ∈d tuỳ ý, dùng eke vẽ đường thẳng c vuông góc với d tại B
Vẽ đường thẳng d’ đi qua A và d’//c
Ta có: d’ ⊥ d.