Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
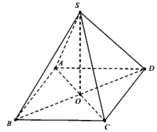
Do hình chóp tứ giác S.ABCD đều nên S O ⊥ A B C D
Mặt khác ABCD là hình vuông nên A C ⊥ B D
Vì A C ⊥ B D A C ⊥ S O ⇒ A C ⊥ S B D , tương tự B D ⊥ S A C .
Suy ra đáp án A, B, D đúng, đáp án B sai.
a) `[S,BC,O]`:
Góc phẳng nhị diện `[S,BC,O`] là góc giữa mặt phẳng `(SBC)` và mặt phẳng `(SBO)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(SBC)` và mặt phẳng `(SBO)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện `[S,BC,O]` là góc vuông.
b) `[C,SO,B]`:
Góc phẳng nhị diện `[C,SO,B]` là góc giữa mặt phẳng `(CSO)` và mặt phẳng `(CSB)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(CSO)` và mặt phẳng `(CSB)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện` [C,SO,B]` là góc vuông.
Chọn C.
Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Chọn C vì điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
mình làm cũng hoang mang lắm bạn=), hay để hỏi cô xem sao
