Biết rằng 1 1 . 2 . 3 1 2 . 3 . 4 . . . 1 n ( n...

PT

Pham Trong Bach

6 tháng 12 2017

Biết rằng 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n ( n ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 12 2017

Đúng(0)

NH

nguyen hoang long

15 tháng 4 2022

biết rằng n! = n x (n-1) x (n-2) x ... x 3 x 2 x 1.Ví dụ, 4! = 4 x 3 x 2 x 1. Tìm số dư trong phép chia tổng 1! + 2! + 3! + ... + 10! cho 20

#Hỏi cộng đồng OLM #Toán lớp 8

1

KK

Kaito Kid

15 tháng 4 2022

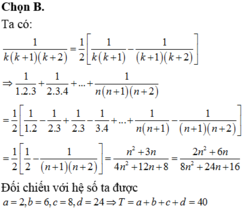
-Từ số 4! đến số 10! đều chia hết cho 20 do có thừa số 4.5=20.

-Mà 1!+2!+3!=1+2+6=91!+2!+3!=1+2+6=9 chia 20 dư 9 nên tổng đó chia 20 dư 9.

Đúng(2)

TT

Trần Tuấn Hoàng

15 tháng 4 2022

-Bạn ạ bạn tham khảo từ bài của mình thì ghi tham khảo nhé!

Đúng(1)

LK

Lâm Khánh Ly

16 tháng 8 2021

Tìm số tự nhiên n , biết rằng :

a) 1+2+3+4+...+n=231

b) 1+3+5+7+...+(2n-1)=169

#Hỏi cộng đồng OLM #Toán lớp 6

2

OY

OH-YEAH^^

16 tháng 8 2021

a) Số số hạng là

(n-1):1+1=n(số)

Ta có: \(\dfrac{\left(n+1\right).n}{2}=231\)

\(\left(n+1\right).n=462\)

n=21

Đúng(1)

LK

Lâm Khánh Ly

16 tháng 8 2021

Giải hộ mình luôn ý b đi

Đúng(0)

EA

Erika Alexandra

5 tháng 2 2017 - olm

Bài 1: Chứng minh rằng A<B<1 biết:

A = 3/1.4+3/4. … . 3/n.(n+1).

B = 1/^2+1/3^2+1/4^2+ … + 1/n^2.

Bài 2: Cho S = 3/10+3/11+3/12+3/13+3/14. Chứng minh rằng 1<S<2. Từ đó suy ra S không phải là số tự nhiên.

Bài 3: Chứng minh rằng 3/5<S<4/5 với S = 1/31+1/32+1/33+…+1/60.

Các bạn nhớ giải đầy đủ và theo cách của Toán lớp 6 nâng cao nhé!

#Hỏi cộng đồng OLM #Toán lớp 6

0

NT

Nguyễn Trúc Phương

20 tháng 10 2016 - olm

tìm n biết rằng:

a,5^n-1+5^n-2=30

b,2^n+2-3.2^n-1=5.2^4

c.3^2n-1+2.9^n-1=135

#Hỏi cộng đồng OLM #Toán lớp 7

0

A

aicohumanchominh

28 tháng 10 2023 - olm

Bài 1: Tìm số tự nhiên nhỏ nhất có 3 chữ số biết rằng khi chia số đó cho 2, 3, 4, 5, 6, 9 thì đều dư là 1. Bài 2: Tìm n biết rằng: a) BCNN của 2 số ( n + 2 ) và ( n + 3) là 143. b) BCNN của 2 số ( 5n + 2) và ( 3n + 1) là 170.

#Hỏi cộng đồng OLM #Toán lớp 6

0

TT

Trần Thị Vân Anh

19 tháng 8 2017 - olm

Cho n số x₁ ,x₂ ,x₃ ,...x_n , mỗi số bằng 1 hoặc -1.Biết rằng tổng của n tích x₁x₂ ,x₂x₃ ,x₃x₄ , ...,x_nx₁ bằng 0. Chứng minh rằng n chia hết cho 4.

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Linh Chi

5 tháng 7 2019

Câu hỏi của Thi Bùi - Toán lớp 7 - Học toán với OnlineMath

Bạn tham khảo link trên nhé!

Đúng(0)

TM

Thảo My

5 tháng 11 2017

Bài 1 : Tìm số tự nhiên n biết rằng :

a) 2n + 1 chia hết cho n - 3

b) n²+ 3 chia hết cho n + 1

Bài 2 : Tìm số tự nhiên n biết rằng :

a) 1 + 2 + 3 + 4 + .... + n = 21

b) 1 + 3 + 5 + 7 + .... + ( 2n - 1 ) = 169

#Hỏi cộng đồng OLM #Toán lớp 6

1

TM

Thảo My

5 tháng 11 2017

Bạn nào giải thì giải chi tiết cho mình nha. Đúng thì mình like, bạn nào giải chi tiết hết được mình kêu bạn bè like cho nha. Mình đang cần gấp nên mong được sự giúp đỡ của các bạn. Cảm ơn ạ <3

Đúng(0)

👁💧👄💧👁

15 tháng 3 2019

Bài 1: Chứng minh rằng: \(\frac{1}{3}-\frac{2}{3^2}+\frac{3}{3^3}-\frac{4}{3^4}+...+\frac{99}{3^{99}}-\frac{100}{3^{100}}< \frac{3}{16}\)

Bài 2: Cho \(n\in N;n>1\). Chứng minh rằng: \(S=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{\left(n-1\right)^2}+\frac{1}{n^2}\notin N\)

#Hỏi cộng đồng OLM #Toán lớp 6

1

👁💧👄💧👁

16 tháng 3 2019

Nguyen svtkvtm Khôi Bùi Nguyễn Việt Lâm Lê Anh Duy Nguyễn Thành Trương DƯƠNG PHAN KHÁNH DƯƠNG An Võ (leo) Ribi Nkok Ngok Bonking ...

Đúng(0)

....

30 tháng 6 2021

chứng minh rằng với số tự nhiên n,n lớn hơn 4 ta có:

\(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+\dfrac{1}{4\sqrt{3}+3\sqrt{4}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}< 1\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NV

Nguyễn Việt Lâm

Giáo viên

30 tháng 6 2021

\(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{\left(n+1\right)^2n-n^2\left(n+1\right)}\)

\(=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{n\left(n+1\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)

Do đó:

\(VT=\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)

\(VT=1-\dfrac{1}{\sqrt{n+1}}< 1\) (đpcm)

Đúng(2)

VM

Võ Mỹ Hảo

30 tháng 8 2018 - olm

1 ) Thực hiện phép tính :
a ) √ 64 + √ 49 / 121 - √ (-9) mũ 2
b ) √ 5 mũ 2 - √ 16 + √ ( - 1 ) mũ 2
c ) √ 4 / 9 + √ 25 / 4 + √ ( -3 ) mũ 4
2 ) Tìm x mũ 2 biết rằng :
a ) √ x = 5
b ) √ x = 4
3 ) Chứng tỏ rằng :
√ 1 + 2 + 3 + ... + ( n - 1 ) + n + ( n - 1 ) + ... + 3 + 2 + 1

#Hỏi cộng đồng OLM #Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP