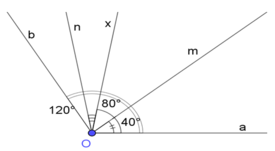
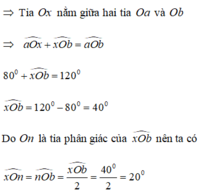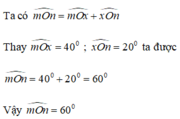Cho góc aOb = 120 độ. Kẻ tia Ox nằm giữa hai tia Oa ; Ob và góc aOx=80 độ.Gọi Om là tia phân giác của góc aOx,On là tia phân giác của góc xOb . Tính số đo các góc mOx, xOn , mOn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2016
x O y t A B
Giải:
Vì Ot là tia phân giác của góc \(\widehat{xOy}\) nên:
\(\widehat{xOt}=\widehat{tOy}=\frac{1}{2}\widehat{xOy}=60^o\)
Vì OB là tia phân giác của góc \(\widehat{tOy}\) nên:
\(\widehat{tOB}=\widehat{BOy}=\frac{1}{2}\widehat{tOy}=30^o\)
Vì OA là tia phân giác của góc \(\widehat{xOt}\) nên:
\(\widehat{xOA}=\widehat{AOt}=\frac{1}{2}\widehat{xOt}=30^o\)
Ta có:
\(OA\in\widehat{xOt}\)
\(OB\in tOy\)
Ot nằm giữa Ox và Oy
\(\Rightarrow\)Ot nằm giữa OA và OB
\(\Rightarrow\widehat{AOt}+\widehat{tOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}=30^o+30^o=60^o\)
Vậy \(\widehat{AOB}=60^o\)
2 tháng 6 2018
trên cùng nửa mặp phẳng bờ chứa tia OA có \(\widehat{AOx}=80^0< \widehat{AOB}=120^0\)
\(\Rightarrow ox\)nằm giữa OB VÀ OA
\(\)Ta có ; \(\widehat{AOx}+\widehat{xOB}=\widehat{AOB}\)
\(\Leftrightarrow80^0+\widehat{xOB}=120^0\)
\(\Leftrightarrow\widehat{xOB}=120^0-80^0=40^0\)
mà Om là tia phân giác góc xOB
\(\frac{\Rightarrow xOB}{2}=mOx=\frac{40^0}{2}=20^0\)
2 tháng 6 2018
Bài giải
Tự vẽ hình
Vi Ox nằm giữa 2 tia OA và OB nên góc AOB = góc AOx + góc xOB
=> \(\widehat{xOB}=\widehat{AOB}-\widehat{AOx}\) => \(\widehat{xOB}=120^0-80^0=40^0\)
Vì Om là tia phân giác của góc xOB nên Om nằm giữa 2 tia Ox và OB và \(\widehat{xOm}=\widehat{mOB}=\frac{\widehat{xOB}}{2}=\frac{40^0}{2}=20^0\)
Vậy \(\widehat{mOx}=20^0\)
