Có 60 chỗ ngồi trên một chuyến tàu. 40% ghế ngồi là trống rỗng. Làm thế nào nhiều ghế trống đang có trong tàu?
Trả lời: Có ghế trống.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2018
Số chỗ ngồi trong chuyến tàu có 8 toa tàu là:
8 x 10 = 80 (ghế)
Số ghế có người ngồi là:
80 - 23 = 57( ghế)
Đáp số 57 ghế
9 tháng 4 2018
8 toa có: 8*10=80 chỗ ngồi
=> Số ghế có người ngồi là: 80-23=57 chỗ ngồi
nha
NM
Nguyễn Minh Quang
Giáo viên
12 tháng 5 2021
gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)
CM
24 tháng 6 2018
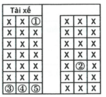
Gọi X là biến cố: "Anh A và chị B ngồi cạnh nhau"
Chọn vị trí cho cặp A, B ngồi có 2 cách là: {3,4}, {4,5}
Xếp A, B vào ghế có 2!
Xếp 3 người còn lại vào 3 vị trí còn lại, có 3! cách.
CM
5 tháng 1 2017
Số phần tử không gian mẫu là: 
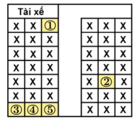
Gọi X là biến cố: " Anh A và chị B ngồi cạnh nhau ".
● Chọn vị trí cho cặp A, B ngồi có 2 cách là: 
Xếp A, B vào ghế có 2!
● Xếp 3 người còn lại vào 3 vị trí còn lại, có: 3! cách
Suy ra số phần tử của biến cố: 
Vậy xác suất cần tính P(X) = 1 5
Chọn C.
11 tháng 4 2021
Gỉa sử đó là gia đình của mình , ta có : bà ngoại là mẹ của mẹ,còn mẹ là mẹ của mình . Vậy có 2 mẹ.
2 con là : mẹ là con của bà,còn mình là con của mẹ vậy kết luận chỉ có 3 người
.
CM
3 tháng 2 2019
Chọn B
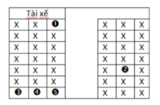
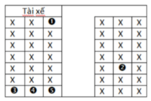
Số cách xếp ngẫu nhiên là 5! cách.
Ta tìm số cách xếp thoả mãn:
+ Chọn 2 vị trí cạnh nhau (3,4) và (4,5) có 2 cách.
+ Xếp A và B vào 2 vị trí cạnh nhau vừa chọn có 2! cách.
+ Xếp 3 người còn lại có 3! cách.
Số cách xếp là 2.2!3!. Xác suất cần tính bằng 
Có 60 chỗ ngồi trên một chuyến tàu. 40% ghế ngồi là trống rỗng. Làm thế nào nhiều ghế trống đang có trong tàu? Trả lời: Có 20 ghế trống.
số ghế trống trên tràu là :
\(60\cdot40\%=24\left(ghế\right)\)