Giải chi tiết giúp e ạ. Em cần gấp!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC





\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)






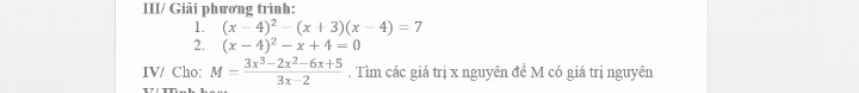
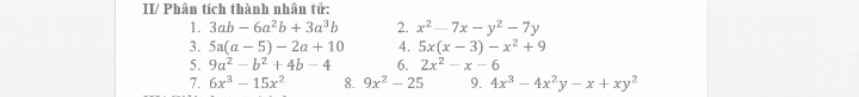


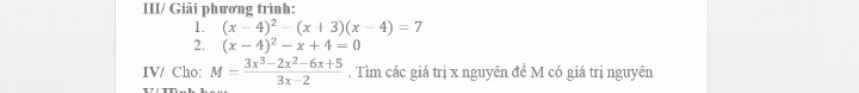
\(a,\Leftrightarrow2x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(b,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3+x>0\\2x-5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\2x-5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{5}{2}\\x< -3\end{matrix}\right.\)
\(c,\Leftrightarrow x\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-3< x< 0\)
\(d,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0\\x+5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\x+5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-3\\x< -5\end{matrix}\right.\)
\(e,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-2x\ge0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-2x\le0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x\le\dfrac{3}{2}\)
b)\(\left(3+x\right)\left(2x-5\right)>0\Leftrightarrow\left\{{}\begin{matrix}3+x>0\\2x-5>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x>\dfrac{5}{2}\end{matrix}\right.\)