Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 3 - 1 và tiếp tuyến của đồ thị này tại điểm - 1 ; - 2
A. S = 4 27
B. S = 4 17
C. S = 17 4
D. S = 27 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 5 2019
Đáp án C
Phương trình tiếp tuyến có dạng y = y ' x 0 . x − x 0 + y 0
⇔ y = 2 x 0 − 4 . x − x 0 + x 0 2 − 4 x 0 + 3
Tiếp tuyến đi qua A 3 2 ; − 3 ⇒ thay A vào phương trình tiếp tuyến :
− 3 = 2 x 0 − 4 . 3 2 − x 0 + x 0 2 − 4 x 0 + 3
⇔ − 3 = 3 x 0 − 2 x 0 2 − 6 + 4 x 0 + x 0 2 − 4 x 0 + 3
x 0 2 − 3 x 0 = 0 ⇔ x 0 = 0 x 0 = 3
+) x 0 = 0 ⇒ tiếp tuyến d 1 : y = − 4 x − 0 + 3
y = − 4 x + 3
+) x 0 = 3 ⇒ tiếp tuyến d 2 : y = 2 x − 3 + 3
y = 2 x − 6
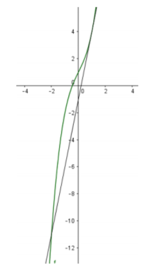
Vẽ đồ thị y = x 2 − 4 x + 3 và hai tiếp tuyến d 1 , d 2
Ta có: S = S 1 + S 2
= ∫ 0 3 2 x 2 − 4 x + 3 − − 4 x + 3 d x + ∫ 0 3 2 x 2 − 4 x + 3 − 2 x − 6 d x = 9 4
CM
7 tháng 9 2018
Đáp án C
Phương trình đường tiếp tuyến tại x = 1 là
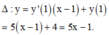
Hoành độ giao điềm của (C) và ∆ là nghiệm của phương trình
Chọn đáp án D