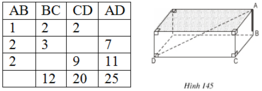
A, B, C, D là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Ta có bảng sau:
CM
23 tháng 10 2019
Trước hết ta chứng minh hệ thức: DA2 = AB2 + BC2 + CD2.
+ ΔBCD vuông tại C suy ra: BD2 = BC2 + CD2 .
+ ΔABD vuông tại B ⇒ AD2 = AB2 + BD2
Mà BD2 = BC2 + CD2 ⇒ AD2 = AB2 + BC2 + CD2 .
Vậy AD2 = AB2 + BC2 + CD2 .
Áp dụng hệ thức trên để tính các cạnh còn thiếu trong bảng ta có:
+ Cột 1: AB = 6; BC = 15; CD = 42
⇒AD2 = AB2 + BC2 + CD2 = 62 + 152 + 422 = 2025
⇒AD = 45.
+ Cột 2: AB = 13; BC = 16; AD = 45
⇒CD2 = AD2 - AB2 - BC2 = 452 - 132 - 162 = 1600
⇒CD = 40.
+ Cột 3: AB = 14; CD = 70; DA = 75
⇒BC2 = DA2 - CD2 - AB2 = 752 - 702 - 142 = 529
⇒BC = 23
+ Cột 4: BC = 34; CD = 62; DA = 75
⇒AB2 = DA2 - BC2 - CD2 = 752 - 342 - 622 = 625
⇒AB = 25.
Vậy ta có kết quả như bảng sau:
| AB | 6 | 13 | 14 | 25 |
| BC | 15 | 16 | 23 | 34 |
| CD | 42 | 40 | 70 | 62 |
| DA | 45 | 45 | 75 | 75 |
CM
8 tháng 9 2019
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)
CM
7 tháng 2 2017
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Công thức liên hệ giữa m,n,d,c :
m = n + 2 ; d = 2n; c = 3n
CM
10 tháng 6 2019
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh
CM
29 tháng 8 2019
| Hình | a | b | c | d |
| Số cạnh của một đáy | 3 | 4 | 6 | 5 |
| Số mặt bên | 3 | 4 | 6 | 5 |
| Số đỉnh | 6 | 8 | 12 | 10 |
| Số cạnh bên | 3 | 4 | 6 | 5 |
PT
1
PT
1
Kết quả:
Cách tính: