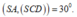Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết V S . A B C D = a 3 3 3 . Tính góc giữa SA và mặt phẳng (SCD).
A. 60 °
B. 45 °
C. 30 °
D. 90 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2023
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
16 tháng 6 2023
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
CM
25 tháng 10 2018
Đáp án A
Do AB // CD => giao tuyến của mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Dễ thấy Sx ⊥ (DSA) => Góc tạo bởi mặt phẳng (SAB) và (SCD) bằng góc D S A ^ = a r c tan 1 3 = 30 0
CM
10 tháng 2 2019
Đáp án C
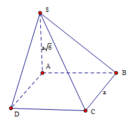
V S . A B C D = 1 3 S . A . d t A B C D = 1 3 a 6 . a 2 = a 3 6 3
Chọn C.
Ta có: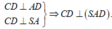
Kẻ AH ⊥ SD, suy ra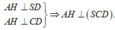
Từ đây ta có: SH là hình chiếu của SA lên (SCD).
Do đó: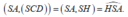
Theo giả thiết ta có:
Xét tam giác SAD vuông tại A, ta có:
Vậy