Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A 6 ; 0 ; 0 , B 0 ; 6 ; 0 , C 2 ; 1 ; 0 và D ( 4 ; 3 ; - 2 ) . Hỏi có bao nhiêu mặt phẳng đi qua hai điểm A, B và cách đều hai điểm C, D.
A. 1
B. 2
C. 3
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2018
Đáp án D
Dễ thấy phương trình mặt phẳng (Oxz): y = 0 nên suy ra điểm đối xứng với A(1; -4; - 5) qua (Oxz) là điểm A'(1;4;-5).
. Tìm tọa độ điểm A.
CM
2 tháng 10 2017
Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
CM
12 tháng 4 2017
Đáp án C.
Ta có vecto chỉ phương của d là
u d ¯ = − 4 ; − 1 ; 2 và
A ' ∈ d ⇒ A ' 6 − 4 a ; − 2 − a ; − 1 + 2 a .
Vì A A ' ¯ . u d ¯ = 0 ⇔ a = 1 ⇒ A ' 2 ; − 3 ; 1 .
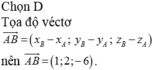
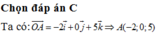
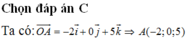
Đáp án B.
Kiểm tra ta được 4 điểm A, B, C, D không đồng phẳng nên tạo nên tứ diện.
- Một mặt phẳng đi qua A, B và song song với CD.
- Một mặt phẳng đi qua A, B và trung điểm CD