Cho hình lăng trụ tam giác đều ABC A'B'C' có A B = 2 3 và A A ' = 2 . Gọi M và N lần lượt là trung điểm của A'C' và A'B'. Tính cosin của góc tạo bởi hai mặt phẳng A B ' C ' và B C M N .
A. 13 65
B. − 13 65
C. 13 130
D. − 13 130
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi L là điểm thỏa mãn A P ¯ = 3 P L ¯ và Q là trung điểm B ' C ' thì cosin cần tìm là
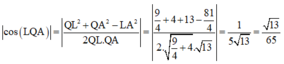

Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B

Gọi D, E, F lần lượt là trung điểm A'A, BC và MN
\(\left\{{}\begin{matrix}MN||B'C'\\DN||AB'\end{matrix}\right.\) (đường trung bình tam giác) \(\Rightarrow\left(AB'C'\right)||\left(DNM\right)\)
\(\Rightarrow\) Góc giữa (AB'C') bằng góc giữa (DNM) và (BCMN)
\(MN\perp A'F\) (A'MN là tam giác đều), và \(A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp MN\)
\(\Rightarrow MN\perp\left(A'AEF\right)\) \(\Rightarrow\) góc giữa (DNM) và (BCMN) là \(\widehat{DFE}\) nếu nó là góc nhọn và \(180^0-\widehat{DFE}\) nếu nó là góc tù
\(MN=\dfrac{1}{2}B'C'=\sqrt{3}\Rightarrow A'F=\dfrac{MN\sqrt{3}}{2}=\dfrac{3}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow DF=\sqrt{A'F^2+A'D^2}=\dfrac{\sqrt{13}}{2}\)
\(AE=\dfrac{AB\sqrt{3}}{2}=3\Rightarrow DE=\sqrt{AD^2+AE^2}=\sqrt{10}\)
Gọi G là trung điểm AE \(\Rightarrow FG\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}FG=A'A=2\\GE=\dfrac{1}{2}AE=\dfrac{3}{2}\end{matrix}\right.\)
\(EF=\sqrt{FG^2+EG^2}=\dfrac{5}{2}\)
Áp dụng định lý hàm cos:
\(cos\widehat{DFE}=\dfrac{DF^2+EF^2-DE^2}{2DF.EF}=...\Rightarrow\widehat{DFE}=...\)
Đáp án A.
Cách 1: Gọi P là giao điểm của BN và A'B'=>P là trọng tâm Δ A ' B ' B .
Q là giao điểm của CM và A'C'=>Q là trọng tâm Δ A ' C ' C
⇒ P Q / / B ' C ' Ta có A B ' C ' ∩ B C M N = P Q .
Gọi H là trung điểm của B'C' và I là giao điểm của AH và PQ.
I là trung điểm của PQ.
Qua I kẻ đường thẳng vuông góc với BC, cắt BC và MN lần lượt tại J và K
=>J là trung điểm BC và K là trung điểm MN.
Ta có A B ' = A C ' ⇒ Δ A B ' C ' cân tại A ⇒ A H ⊥ B C ⇒ A I ⊥ P Q .
Lại có I J ⊥ P Q ⇒ Góc giữa A B ' C ' và B C M N là góc giữa IJ và IA.
Ta có:
A C ' = A C 2 + C C ' 2 = 2 3 2 + 2 2 = 4
⇒ A H = A C ' 2 − H C ' 2 = 4 2 − 3 2 = 13 ⇒ A I = 2 3 A H = 2 13 3
B N = B B ' 2 + B ' N 2 = 2 2 + 3 2 = 7
K J = N E = B N 2 − E B 2 = 7 − 3 4 = 5 2 ⇒ I J = 2 3 K J = 5 3
Lại có A J = 2 3 . 3 2 = 3
Trong Δ A I J :
cos A I J ^ = I J 2 + I A 2 − A J 2 2. I J . I A = 25 9 + 4.13 9 − 9 2. 5 3 . 2 13 3 = − 13 65 .
Cosin của góc giữa A B ' C ' và B C M N là 13 65
Cách 2: (Tọa độ hóa)
Gọi T là trung điểm AC. Đặt M = 0 ; 0 ; 0 , B ' 3 ; 0 ; 0 , C ' 0 ; 3 ; 0 , T 0 ; 0 ; 2
⇒ A 0 ; − 3 ; 2 , B 3 ; 0 ; 2 , C 0 ; 3 ; 2 ⇒ M B → = 3 ; 0 ; 2 , M C → = 0 ; 3 ; 2
n → = M B → , M C → = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của .
Lại có A B ' → = 3 ; 3 ; − 2 , A C ' → = 0 ; 2 3 ; − 2
⇒ n ' → = A B → , A C → ' = 2 3 ; 6 ; 6 3 là một vecto pháp tuyến của A B ' C ' .
Gọi α là góc giữa A B ' C ' và M N B C .
Ta có:
cos α = cos n → ; n ' → ^ = − 2 3 .2 3 + − 6 .6 + 3 3 .6 3 − 2 3 2 + − 6 2 + 3 3 2 . 2 3 2 + 6 2 + 6 3 2 = 13 65