Một bếp điện hoạt động bình thường khi được mắc với hiệu điện thế 220V và khi đó bếp có điện trở 48,4Ω.Tính công suất điện của bếp này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công suất của bếp điện là:
\(P=\dfrac{U^2}{R}=\dfrac{220^2}{48,4}=1000\left(W\right)\)
Công suất điện của bếp này là
P = =
= 1000W.

a)Công suất điện trở:
\(P=\dfrac{U^2}{R}=\dfrac{220^2}{50}=968W\)
b)Công suất tiêu thụ trong 30 ngày:
\(\Sigma P=968\cdot6\cdot3600\cdot30=627264000W=174,24kW\)
Gía tiền cần trả:
\(T=174,24\cdot2800=487872\left(đồng\right)\)

Cường độ dòng điện qua bếp: I = U/R = 220/48,4=50/11A
Công suất của bếp điện:
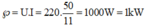

Chọn C
Gọi R0, ZL, ZC là điện trở thuần, cảm kháng và dung kháng của quạt điện.
Công suất định mức của quạt P = 120W, dòng điện định mức của quạt I. Gọi R2 là giá trị của biến trở khi hoạt động bình thường khi điện áp U = 220V.
Khi biến trở có giá trị R1 = 70Ω thì I1 = 0, 75A, P1 = 0, 928P = 111, 36W
P1=I12R0 (1) => R0 = P1/I12 ≈ 198Ω (2)
I1 = U Z 1 = U R 0 + R 1 2 + Z L - Z C 2 = 220 268 2 + Z L - Z C 2
Suy ra : Z L - Z C 2 = 220 0 , 75 2 – 2682 => |ZL – ZC| ≈ 119Ω (3)
Khi bếp điện hoạt động bình thường, ta có: P=I2R0 =120W (4)
Với I = U Z = U R 0 + R 2 2 + Z L - Z C 2 (5)
P = U 2 R 0 R 0 + R 2 2 + Z L - Z C 2 => R0 + R2 ≈ 256Ω => R2 ≈ 58 Ω
R2 < R1 => ∆R = R2 – R1 = -12Ω
Phải giảm 12Ω

TT
\(U=220V\)
\(R=48,4\Omega\)
\(t=1h\)
\(A=?Wh=kWh\) = số
Giải
Công suất điện của bếp điện là
\(P\left(hoa\right)=\dfrac{U^2}{R}=\dfrac{220^2}{48,4}=1000W\)
Điện năng tiêu thụ của bếp điện là;
\(A=P\left(hoa\right).t=1000.1=1000Wh=1kWh\)
Điện năng tiêu thụ ứng với 1 số đếm của công tơ điện

a. A = 2,4 số = 2,4kWh = 2400Wh
b. \(\left\{{}\begin{matrix}A=Pt\Rightarrow P=\dfrac{A}{t}=\dfrac{2400}{1,8}=\dfrac{4000}{3}W\\R=U^2:P=220^2:\dfrac{4000}{3}=36,3\left(\Omega\right)\end{matrix}\right.\)
câu a nếu dc thì bạn tính ra J nhá, đáp án thầy mình cho là thế ạ
\(P=\dfrac{U^2}{R}=\dfrac{220^2}{48,4}=1000\)W