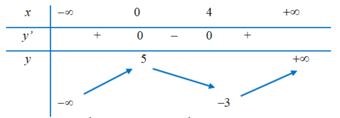
Cho hàm số y = f(x) liên tục trên và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là sai?
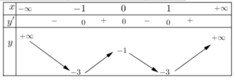
A. Hàm số có giá trị lớn nhất bằng -1.
B. Hàm số có hai điểm cực tiểu, một điểm cực đại.
C. Hàm số đồng biến trên khoảng (1;3).
D. Hàm số có giá trị nhỏ nhất bằng -3.

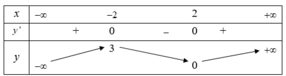
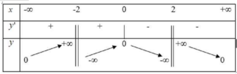

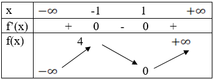
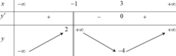

Chọn A
Từ bảng biến thiên, ta có
Hàm số có hai điểm cực tiểu x = -1, x = 1 và một điểm cực đại x = 0.
Hàm số đồng biến trên khoảng (1;+ ∞ ) nên hàm số đồng biến trên (1;3).
Hàm số có giá trị nhỏ nhất bẳng -3.
Từ bảng biến thiên, ta có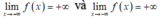 nên hàm số không có giá trị lớn nhất.
nên hàm số không có giá trị lớn nhất.