Một trường THPT có 18 học sinh giỏi toàn diện, trong đó có 11 học sinh khối 12, 7 học sinh khối 11. Chọn ngẫu nhiên 6 học sinh trên để đi dự trại hè. Xác suất để mỗi khối có ít nhất 1 học sinh được chọn là
A. 2558/2652
B. 2585/2652
C. 2855/2652
D. 2559/2652


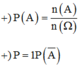
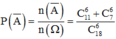
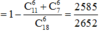

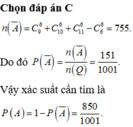
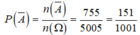
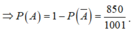 0
0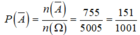
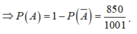
Chọn đáp án B.