Cho hình cầu (O;R) hai mặt phẳng (P) và (Q) song song với nhau, cách đều O, đồng thời cắt khối cầu thành ba phần sao cho thể tích phần nằm giữa hai mặt phẳng bằng
13
27
thể tích khối cầu .Tính khoảng cách giữa (P) và (Q). A.
3
R
2
B.
R
3
C.
2
R
3
D.
R
2
...
Đọc tiếp
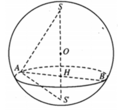
Cho hình cầu (O;R) hai mặt phẳng (P) và (Q) song song với nhau, cách đều O, đồng thời cắt khối cầu thành ba phần sao cho thể tích phần nằm giữa hai mặt phẳng bằng 13 27 thể tích khối cầu .Tính khoảng cách giữa (P) và (Q).
A. 3 R 2
B. R 3
C. 2 R 3
D. R 2
(
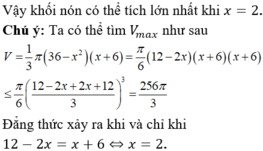
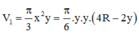
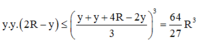
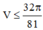
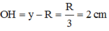
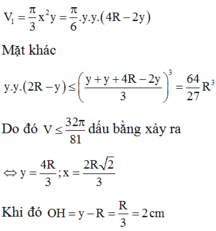
Đáp án C
Ta có công thức chỏm hình cầu bán kính R và chiều cao h là: V = πh 2 R - h 3
Vò 2 mặt phẳng (P) và (Q) song song với nhau, cách đều O nên thể tích phần giữa và thể tích khối cầu được tính là V 1 V c = 4 πR 3 3 - 2 πh 2 R - h 3 4 πR 3 3 = 13 27 ⇔ 14 27 = 3 h 2 2 R 2 - h 3 2 R 3 ⇔ h R = 2 3 v ì 0 < h < R
Khoảng cách giữa (P) và (Q) là 2 R - 2 h = 2 R 3 .