Một sợi dây AB dài 1m căng ngang, hai đầu cố định. Trên dây có sóng dừng ổn định với tần số 80 Hz. Tốc độ truyền sóng trên dây là 20 m/s. Điểm M trên dây cách A là 4 cm. Trên dây còn bao nhiêu điểm cùng biên độ và cùng pha với M?
A. 6
B. 7
C. 14
D. 12

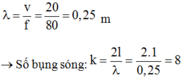
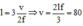
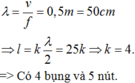
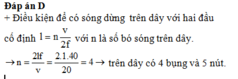
Đáp án B.
Bước sóng λ = v f = 25 c m
Điều kiện để có sóng dừng trên dây với hai đầu cố định là : I = n v 2 f ⇒ n = 2 I f v = 8
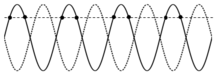
Vậy trên dây có sóng dừng với 8 bó sóng
Các bó sóng liên tiếp nhau sẽ dao động ngược pha nha
Vậy sẽ có 7 điểm dao động cùng biên độ và cùng pha với M