Cho hàm số với a, b là các số hữu tỉ thỏa mãn điều kiện Tính T = a + b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=\(\frac{x^2y^2+x^2z^2+y^2z^2}{x^2y^2z^2}\)
Ta có:\(x^2y^2+x^2z^2+y^2z^2=\left(xy+yz+zx\right)^2-2\left(xyz\right)\left(x+y+z\right)\)
\(=\left(xy+yz+zx\right)^2\)(do x+y+z=0)
Do đó A=\(\frac{\left(xy+yz+zx\right)^2}{\left(xyz\right)^2}=\left[\frac{\left(xy+yz+zx\right)}{xyz}\right]^2\)
Nên A là số chính phương(ĐCCM)

Mình nghĩ như thế này thôi nhé
x+2/x-6 = x-6+8/x-6 = 1 + 8/x-6
để x+2/x-6 là số hữu tỉ dương => x-6 thuộc Ư(8)={ -1 ; 1 ; 2 ; -2 ; 4 ; -4 ; 8 ; -8 }
nếu x -6 = 1 => x = 7 ( TM )
Nếu x - 6 = -1 => x= 8 ( tm )
Nếu x - 6 = 2 => x = 8 ( tm )
Nếu x -6 = -2 => x = 4 ( tm )
Nếu x - 6 = 4 => x = 10 ( tm )
Nếu x -6 = -4 => x = 2 ( tm)
Nếu x -6 = 8 => x = 14 ( tm )
Nếu x -6=-8 => x = -2 ( ktm )
Vậy x € { 7 ; 5 ; £ ; 4 ; 2 ; 10 ; 14 } thì x+2 / x-6 là số hữu tỉ dương
b/ câu này bạn cũng làm tương tự như vậy nhưng x phải là số âm thì mới thỏa mãn .
a)\(\frac{x+2}{x-6}\)là số hữu tỉ dương\(\Leftrightarrow x+2\)và \(x-6\)cùng dấu.
Mà x + 2 > x - 6 nên \(\hept{\begin{cases}x+2< 0\\x-6>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< -2\\x>6\end{cases}}\)
Vậy x < - 2 và x > 6 thì \(\frac{x+2}{x-6}\)là số hữu tỉ dương

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Ta có: \(a=b+c\Rightarrow c=a-b\)
\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\sqrt{\dfrac{b^2c^2+a^2c^2+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{b^2\left(a-b\right)^2+a^2\left(a-b\right)^2+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{b^4+a^2b^2-2ab^3+a^4+a^2b^2-2a^3b+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{\left(a^2+b^2\right)^2-2ab\left(a^2+b^2\right)+a^2b^2}{a^2b^2c^2}}=\sqrt{\dfrac{\left(a^2+b^2-ab\right)^2}{a^2b^2c^2}}=\left|\dfrac{a^2+b^2-ab}{abc}\right|\)
=> Là một số hữu tỉ do a,b,c là số hữu tỉ

Câu 1 :
\(a,2\left(\frac{3}{4}-5x\right)=\frac{4}{5}-3x\)
\(\Rightarrow\frac{3}{2}-10x=\frac{4}{5}-3x\)
\(\Rightarrow7x=\frac{3}{2}-\frac{4}{5}\)
\(\Rightarrow7x=\frac{7}{10}\)\(\Leftrightarrow x=0,1\)
\(b,\frac{3}{2}-4\left(\frac{1}{4}-x\right)=\frac{2}{3}-7x\)
\(\Rightarrow\frac{3}{2}-1+4x=\frac{2}{3}-7x\)
\(\Rightarrow11x=\frac{2}{3}+1-\frac{3}{2}\)
\(\Rightarrow11x=\frac{4+6-9}{6}-\frac{1}{6}\)
\(\Rightarrow x=\frac{1}{66}\)
Câu 2 :
\(a,\frac{2}{x-1}< 0\)
Vì \(2>0\Rightarrow\)để \(\frac{2}{x-1}< 0\)thì \(x-1< 0\Leftrightarrow x< 1\)
\(b,\frac{-5}{x-1}< 0\)
Vì \(-5< 0\)\(\Rightarrow\)để \(\frac{-5}{x-1}< 0\)thì \(x-1>0\Rightarrow x>1\)
\(c,\frac{7}{x-6}>0\)
Vì \(7>0\Rightarrow\)để \(\frac{7}{x-6}>0\)thì \(x-6>0\Rightarrow x>6\)
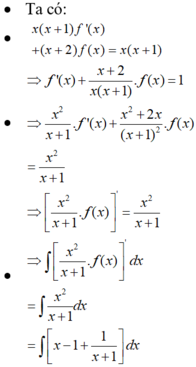
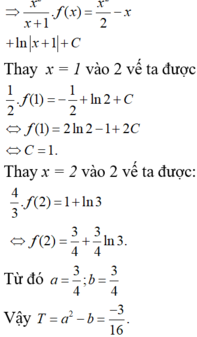
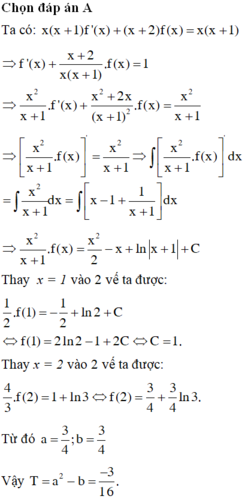
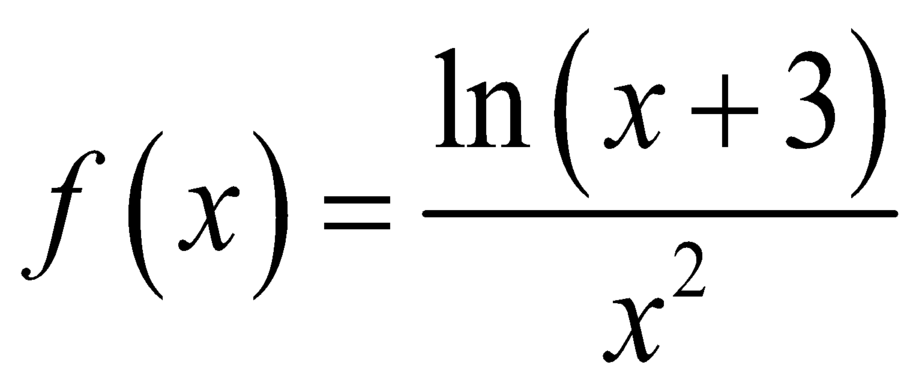
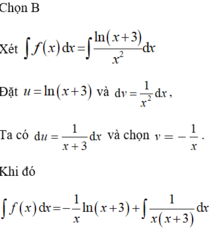

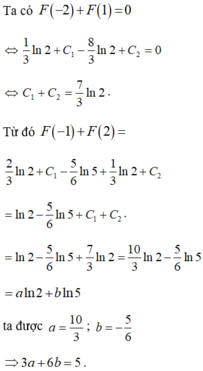

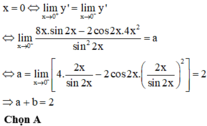
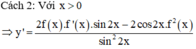
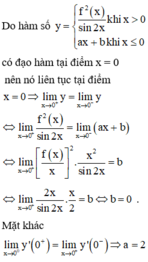
Chọn A.