Trong không gian với hệ tọa độ Oxyz, cho đường thẳng đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Ta có (P) qua O(0;0;0) và nhận BA → = ( 1 ; 3 ; - 5 ) là một VTPT
⇒ ( P ) : x + 3 y - 5 z = 0 .

Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng Δ: 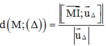 với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
với
u
△
→
là 1 VTCP của Δ và I
∈
Δ là 1 điểm bất kì
Cách giải: Đường thẳng Δ nhận ![]() là 1 VTCP
là 1 VTCP
Gọi M(a;b;0)
∈
(Oxy) => 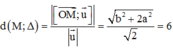
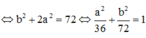
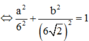
Như vậy tập hợp các điểm M là elip có phương trình 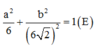
![]()

Đáp án B
Phương pháp: (P) cách đều B, C
![]()
TH1: BC//(P)
TH2: I ∈ (P)với I là trung điểm của BC.
Cách giải:
![]()
(P) cách đều B, C
![]()
TH1: BC//(P)
![]()
=> (P) đi qua O và nhận b → = ( 6 ; - 3 ; - 4 ) là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC.
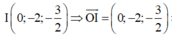
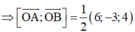
![]()
Dựa vào các đáp án ta chọn được đáp án B.

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
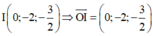
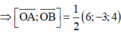
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B

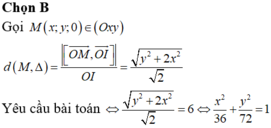



Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng
là 1 điểm bất kì
Cách giải:
là một VTCP
Như vậy tập hợp các điểm M là elip có phương trình