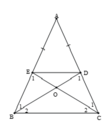
Cho tam giác ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho DB = EC < DE.
a)Chứng minh tam giác ABC là tam giác cân
b)Kẻ BM vuông góc với AD, kẻ CN vuông góc với AE. Chứng minh rằng BM= CN
c)Gọi I là giao điểm của MB và NC. Chứng minh tam giác IBC là tam giác cân.
d) Chứng minh rằng AI là tia phân giác của góc A |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

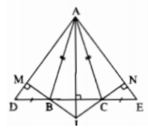
Do ΔADE cân tại A nên ∠D =∠E
Xét ΔABD và ΔACE, ta có:
AD = AE (gt)
∠D =∠E (chứng minh trên)
DB=EC (gt)
Suy ra: ΔABD= ΔACE(c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy: ΔABC cân tại A

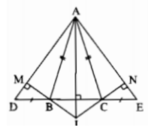
Xét ΔABI và ΔACI, ta có:
AB = AC (chứng minh trên)
IB = IC ( vì ΔIBC cân tại I)
AI cạnh chung
Suy ra: ΔABI= ΔACI(c.c.c) =>∠BAI =∠CAI ̂(hai góc tương ứng)
Vậy AI là tia phân giác của góc ∠BAC

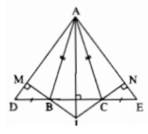
Ta có: ΔBMD=ΔCNE(chứng minh trên)
Suy ra: ∠DBM =∠ECN (hai góc tương ứng)
Lại có: ∠DBM =∠IBC (đối đỉnh) và ∠ECN =∠ICB (đối đỉnh)
Suy ra: ∠IBC =∠ICB hay ΔIBC cân tại I

Xét hai tam giác vuông BMD và CNE, ta có:
∠(BMD) = ∠(CNE) =90o
BD = CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBMD= ΔCNE(cạnh huyền,góc nhọn)
Do đó,BM = CN ( hai cạnh tương ứng).

a: Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ADB}=\widehat{AEC}\)
DB=EC
Do đó: ΔADB=ΔAEC
Suy ra: AB=AC
hay ΔABC cân tại A
b: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
BD=CE
\(\widehat{MDB}=\widehat{NEC}\)
Do đó: ΔMBD=ΔNCE
Suy ra: BM=CN
c: \(\widehat{IBC}=\widehat{MBD}\)(đối đỉnh)
\(\widehat{ICB}=\widehat{NCE}\)
mà \(\widehat{MBD}=\widehat{NCE}\)(ΔMBD=ΔNCE)
nên \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I

a: Xet ΔABD và ΔACE có
AD=AE
góc D=góc E
DB=EC
=>ΔABD=ΔACE
=>AB=AC
=>ΔABC cân tại A
b: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc MAB=góc NAC
=>ΔAMB=ΔANC
=>BM=CN
c: góc IBC=góc MBD
góc ICB=góc NCE
mà góc MBD=góc NCE
nên góc ICB=góc IBC
=>ΔIBC cân tại I

a) Xét △ABD và △ACE có:
AB = AC (gt)
\(\widehat{A}\) chung
AD = AE (gt)
\(\Rightarrow\)△ABD = △ACE (c.g.c)
\(\Rightarrow\)DB = EC (cặp cạnh tương ứng)
b) Ta có :△ABD = △ACE
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\) (cặp góc tương ứng)
Mà \(\widehat{ABC}=\widehat{ACB}\) ( △ABC cân tại đỉnh A)
\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\)△OBC cân tại đỉnh O
\(\Rightarrow\)OB = OC
Ta có: DB = EC (cmt)
OB = OC
\(\Rightarrow\)DB - OB = EC - OC
\(\Rightarrow\)OE = OD
\(\Rightarrow\)△ODE cân đỉnh O (ĐPCM)
c) △OBC cân tại đỉnh O
\(\Rightarrow\)\(\widehat{OCB}=\frac{180^o-\widehat{BOC}}{2}\)
△ODE cân tại đỉnh O
\(\Rightarrow\widehat{DEO}=\frac{180^o-\widehat{DOE}}{2}\)
Mà \(\widehat{BOC}=\widehat{DOE}\)(đối đỉnh)
\(\Rightarrow\widehat{DEO}=\widehat{OCB}\)
Vì 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\)DE // BC (ĐPCM)