Cho tam giác ABC cân tại A, \(\widehat{B}\) = 30o , AC= 5CM. Tính BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AC=\sin B\cdot BC=\dfrac{1}{2}\cdot18=9\left(cm\right)\)

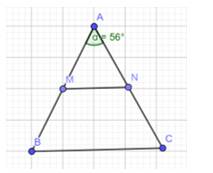
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC

sửa lại :
Cho tam giác ABC cân tại A, \(\widehat{A}=30^o\). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).
Gọi I là giao điểm của BH và CK.
Tính số đo góc \(\widehat{BAI}\)
giải:
ta có : \(\Delta ABC\)cân tại A
=> AB=AC(t/c \(\Delta\)cân)
xét \(\Delta BAH\)và\(\Delta CAK\)
\(\widehat{A}-chung\)
AB=AC
\(\widehat{AKC}=\widehat{AHB}=90^o\)
=>\(\Delta BAH\)=\(\Delta CAK\)(ch-gn)
=>\(\widehat{ABH}=\widehat{ACK}\left(2ctu\right)\)
=>\(\widehat{ABI}=\widehat{ACI}\)
xét \(\Delta ABI\)VÀ \(\Delta ACI\)
AB=AC(cmt)
\(\widehat{ABI}=\widehat{ACI}\)(cmt)
AI-cạnh chung
=>\(\Delta ABI\)=\(\Delta ACI\)(cgc)
=>\(\widehat{BAI}=\widehat{CAI}\left(2gtu\right)\)
ta có : \(\widehat{BAI}+\widehat{CAI}=\widehat{A}=30^o\)
mà\(\widehat{BAI}=\widehat{CAI}\left(cmt\right)\)
=> \(\widehat{BAI}=\widehat{CAI}=15^o\)

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
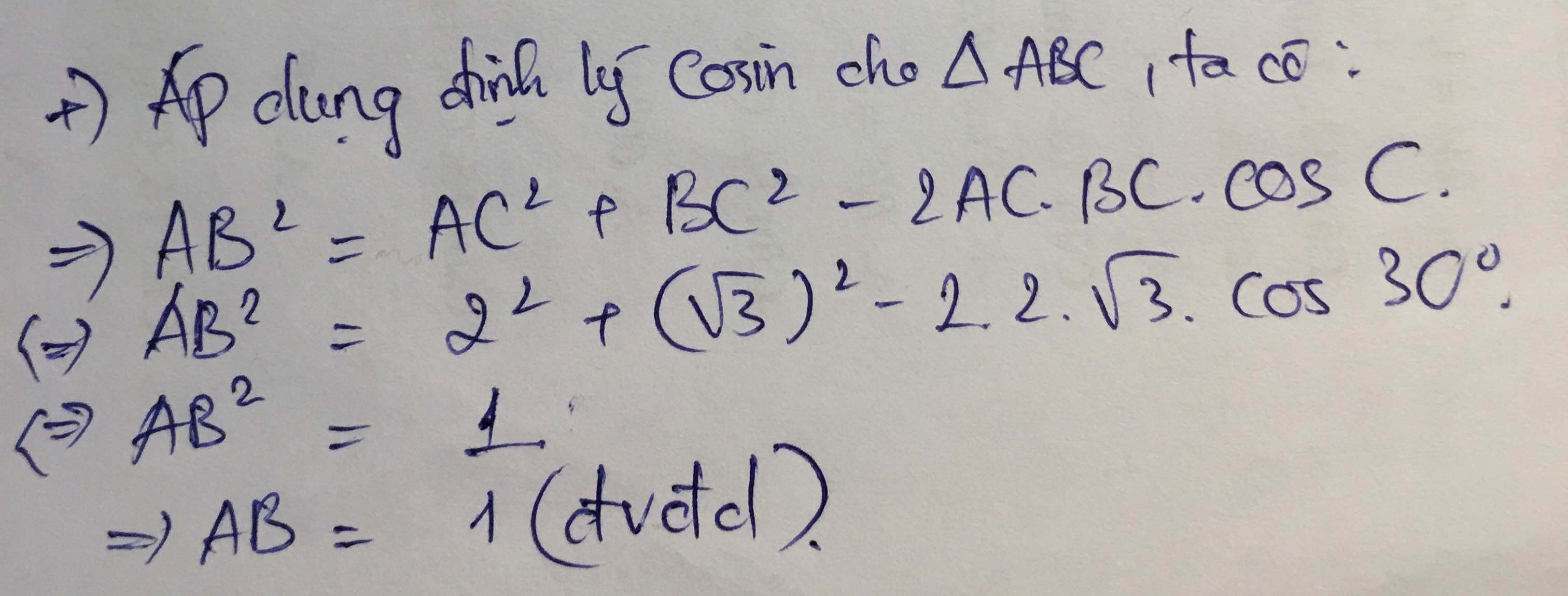
\(AC=AB=5\left(cm\right)\)
Kẻ đường cao AH thì AH cũng là trung tuyến
\(\Rightarrow BH=\dfrac{1}{2}BC=\cos B\cdot AB=\dfrac{\sqrt{3}}{2}\cdot5=\dfrac{5\sqrt{3}}{2}\\ \Rightarrow BC=2\cdot\dfrac{5\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
Thank you bạn nha!!