Cho tam giác MAB cân tại M. Trên tia đối của tia MB lây điểm C sao cho MC = MB. Tính số đo góc BAC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
TC
11 tháng 2 2020
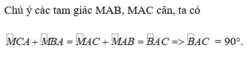
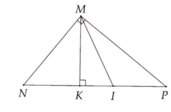
\(\Delta ABM\)cân tại \(M\)
\(=>\hept{\begin{cases}MAB=MBA\\MA=MB< =>MC=MA\end{cases}}\)
\(=>\Delta AMC\)cân tại \(M\)
\(=>MCA=MAC\)
Xét \(\Delta ABM\)có
\(AMB+MAB+MBA=180^0\)
\(=>2MAC+2MAB=180^0\)
\(=>2CAB=180^0\)
\(=>CAB=90^0\)
25 tháng 3 2020
Xét ΔMAC có MA=MC(=MB)
nên ΔMAC cân tại M(định nghĩa tam giác cân)
⇒\(\widehat{C}=\widehat{CAM}\)(hai góc ở đáy)(1)
Ta có: ΔMAB cân tại M(gt)
⇒\(\widehat{B}=\widehat{BAM}\)(hai góc ở đáy)(2)
Ta có: \(\widehat{CAM}+\widehat{BAM}=\widehat{CAB}\)(tia AM nằm giữa hai tia AB,AC)(3)
Từ (1), (2) và (3) suy ra \(\widehat{C}+\widehat{B}=\widehat{BAC}\)
Xét ΔCAB có
\(\widehat{C}+\widehat{B}+\widehat{BAC}=180^0\)(định lí tổng ba góc trong một tam giác)
hay \(2\cdot\widehat{BAC}=180^0\)
⇔\(\widehat{BAC}=90^0\)
Vậy: \(\widehat{BAC}=90^0\)
DN
25 tháng 3 2020
Ta có: AM là đường trung tuyến ΔABCΔABC
MB=MC=AM
BC=MB+MC=2MC=2AM
Suy ra \(AM=\frac{1}{2}BC\) (Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Vậy ΔABC cân tại A hay \(\widehat{BAC}=90^o\)
JK
23 tháng 4 2020
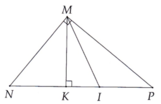
hình của mjnh thiếu điểm H và K rồi bạn tự thêm vào đi
a, tam giác MND cân tại M (gt)
=> ^MND = ^MDN (tc)
^MND + ^MNB = 180 (kb)
^MDN + ^MDA = 180 (kb)
=> ^MNB = ^MDA
xét tam giác MNB và tam giác MDA có BN = DA (gt)
MN = MD do tam giác MND cân tại M (gt)
=> tg MNB = tg MDA (c-g-c)
=> MA = MB (đn)
=> tg MAB cân tại M (Đn)
b, xét tam giác DHA và tam giác NKB có : AD = BN (gt)
^AHD = ^BKN = 90
^A = ^B do tam giác MAB cân tại M (câu a)
=> tg DHA = tg NKB (ch-gn)
=> DH = KN (đn)
c, tg DHA = tg NKB (câu b)
=> AH = KB (đn)
có MA = MB (câu a)
AH + MH = AM
MK + KB = BM
=> MH = MK
d, có ^HDA = ^KNB do tg DHA = tg NKB (Câu b)
^HDA = ^NDI (đối đỉnh)
^KNB = ^DNI (đối đỉnh)
=> ^NDI = ^DNI
=> tam giác DNI cân tại I
HK
0
10 tháng 2 2022
a: Đề sai rồi bạn
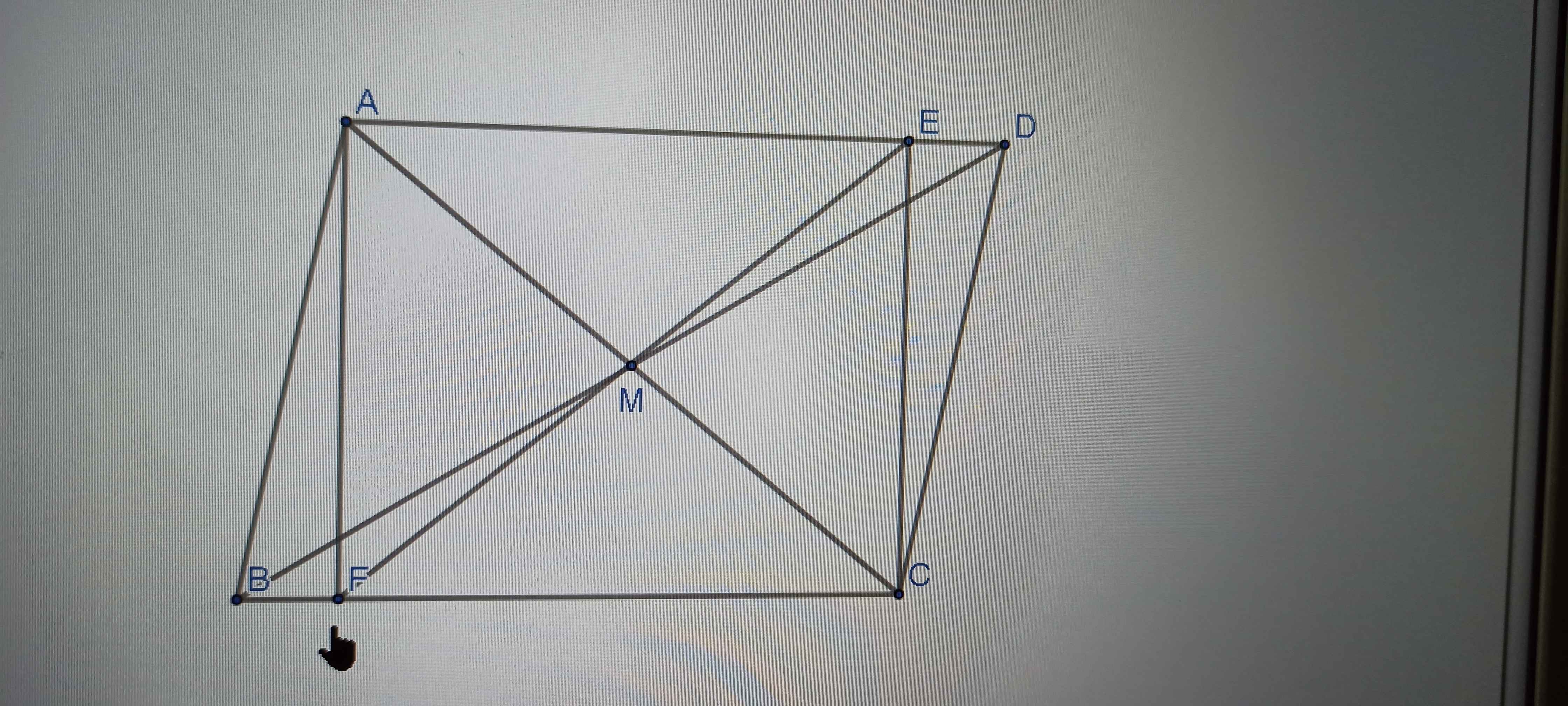
b: Xét ΔAMB và ΔCME có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)
MB=ME
Do đó: ΔAMB=ΔCME
16 tháng 7 2021
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.