Tìm giá trị nhỏ nhất của hàm số y = x 3 - 3 x 2 - 9 x + 5 trên đoạn - 2 ; 2
A. 3.
B. -22.
C. -1.
D. -17.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
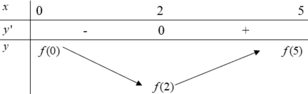
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.

y = (x² - 1)(x + 3)(x + 5)
= [(x - 1)(x + 5)].[(x + 1)(x + 3)]
= (x² + 4x - 5)(x² + 4x + 3)
= [x² + 4x - 1) - 4].[(x² + 4x - 1) + 4]
= (x² + 4x - 1)² - 16 ≥ - 16
- Khi x = 0 ⇒ y = - 15
- Khi x = 1 ⇒ y = 0
- Khi x² + 4x - 1 = 0 ⇔ x = √5 - 2 ( loại giá trị x = - √5 - 2 < 0) ⇒ y = - 16
Vậy trên đoạn [0; 1] thì :
GTNN của y = - 16 khi x = √5 - 2
GTLN của y = 0 khi x = 1

Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.
Chọn D.
Hàm số y = x 3 - 3 x 2 - 9 x + 5 liên tục trên - 2 ; 2