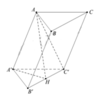
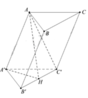
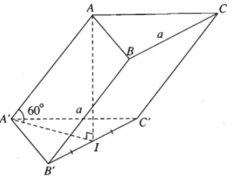
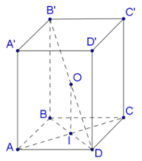
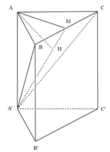
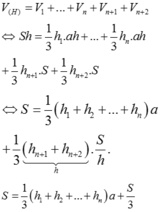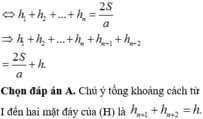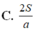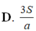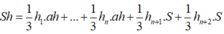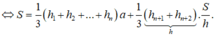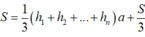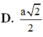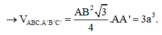Cho hình lăng trụ đều có độ dài cạnh đáy bằng a. Chiều cao của hình lăng trụ bằng h, diện tích một mặt đáy bằng S. Tổng khoảng cách từ một điểm trong của hình lăng trụ đến tất cả các mặt của hình lăng trụ bằng
A. h + 2 S a
B. h + 3 S a
C. 2 S a
D. 3 S a