Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính của mặt cầu ngoại tiếp hình nón đó là
Trong không gian a và b có thể cắt nhau và cùng thuộc mặt phẳng song song với mặt phẳng đã cho.
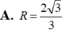
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Thiết diện qua trục là tam giác đều cạnh 2.
Khi đó bán kính của mặt cầu ngoại tiếp hình nón đó là: R = R Δ = a 2 sin A = 2 2 sin 60 ° = 2 3 3

Dựng mặt phẳng (Q) chứa đường cao SO của hình chóp
Ta được thiết diện là tam giác SAB như hình vẽ
\(\Rightarrow OI=h;OA=OB=R;\widehat{ASO}=\widehat{BSO=\alpha}\)
(P) cắt (Q) qua giao tuyến MN, MN cắt SO tại điểm I \(\Rightarrow\) IM=IN=r (bán kính đường tròn (C) )
Tam giác SIN đồng dạng với tam giác SOB
\(\Rightarrow\frac{SI}{SO}=\frac{IN}{OB}\Leftrightarrow IN=\frac{SI.OB}{SO}=\frac{\left(SO-MO\right).OB}{SO}=\frac{\left(OB.cot\widehat{OSB}-MO\right).OB}{OB.cot\widehat{OSB}}\\ \Rightarrow r=\frac{Rcot\alpha-h}{Rcot\alpha}=1-\frac{h}{Rcot\alpha}\)