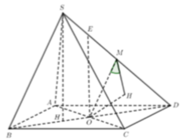
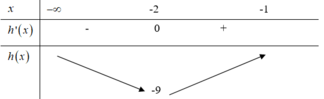
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc BAD có số đo bằng 60 o . Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng . Tính khoảng cách từ B đến mặt phẳng (SCD) .
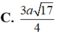
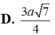
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
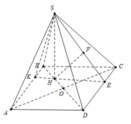
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Chọn đáp án A

Từ kẻ đường thẳng vuông góc với SC cắt SC tại K.
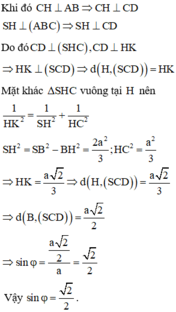


Đáp án là A.

d B ; S C D = 3 2 d G ; S C D
Tính được: G H = a 3 3 ; S G = a 2 ; G K = a 7 .
Vậy d B ; S C D = 3 2 d G ; S C D = 3 2 . a 7 = 3 a 2 7 .

Chọn D.
Phương pháp:
- Gọi M là trung điểm của SD, nhận xét góc giữa SB và (SCD) cũng bằng góc giữa OM và (SCD).
- Xác định góc φ và tính sin φ
Cách giải: