Trong không gian Oxyz, cho các điểm A(2;3;3), B(−2;−1;1). Gọi S1 và (S2) lần lượt là hai mặt cầu thay đổi nhưng luôn tiếp xúc với đường thẳng AB lần lượt tại các điểm A, B; đồng thời tiếp xúc ngoài với nhau tại điểm M(a;b;c). Khi khoảng cách từ điểm M đến mặt phẳng (P): x+2y-2z+2018=0 đạt giá trị lớn nhất, giá trị biểu thức a+b+c bằng
A. 4
B. 5
C. 3
D. 2

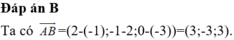
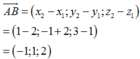
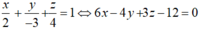
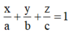



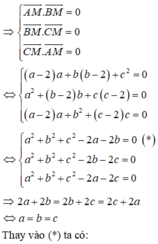


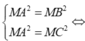
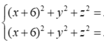
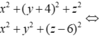
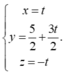
Gọi I1, I2, R1, R2 lần lượt là tâm và bán kính của các mặt cầu (S1) và (S2). Theo điều kiện tiếp xúc có I 1 A = R 1 ; I 2 B = R 2 .
Mặt khác hai mặt cầu tiếp xúc ngoài với nhau tại điểm M nên I 1 I 2 = R 1 + R 2 = I 1 A + I 2 B ⇒ I 1 I 2 luôn tiếp xúc với mặt cầu đường kính AB tại điểm M tức là M thuộc mặt cầu đường kính AB
Phương trình mặt cầu đường kính AB là ( S ) : x 2 + y - 1 2 + z - 2 2 = 9 có tâm I(0;1;2), R = 3.
Vì vậy M ∈ ( S ) ⇒ d M , P ≤ d I , P + R
=672+3=675.
Gọi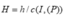
Dấu bằng đạt tại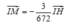
Chọn đáp án A.