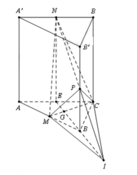
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A'C’, BB’. Thể tích của khối tứ diện CMNP bằng
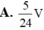
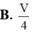
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


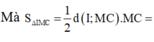

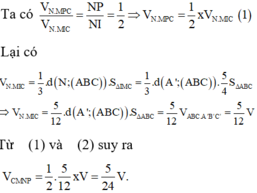

Đáp án A
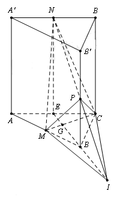
Gọi E là trung điểm của A C ⇒ N E / / B B ' . Nối NP cắt BE tại I suy ra B là trung điểm của EI. Gọi G là trọng tâm của tam giác ABC ⇒ B G = 2 E G .
⇒ d B ; M C = 2 d E ; M C ⇒ d B ; M C = 2 3 d B ; A C
Suy ra: d I ; M C = 1 + 3 2 d B ; M C = 5 2 d B ; M C
Mà S Δ I M C = 1 2 d I ; M C . M C
= 1 2 . 5 2 d B ; M C . M C = 5 2 S Δ M B C = 5 4 S Δ A B C
Ta có: V N . M P C V N . M I C = N P N I = 1 2 ⇒ V N . M P C = 1 2 x V N . M I C 1
Lại có:
V N . M I C = 1 3 . d N ; A B C . S Δ I M C = 1 3 . d A ' ; A B C . 5 4 S Δ A B C ⇒ V N . M I C = 5 12 . d A ' ; A B C . S Δ A B C = 5 12 V A B C . A ' B ' C ' = 5 12 V
Từ (1) và (2) suy ra V C M N P = 1 2 . 5 12 x V = 5 24 V .

Đáp án B
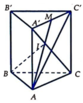
Xét ∆ A A ' C có I là trọng tâm, d ( I , ( A B C ) ) = 2 3 d ( M , ( A B C ) )
Ta có: V A B C . A ' B ' C ' = S A B C . A A ' = S A B C . d A ' ; A B C
V I A B C = 1 3 S ∆ A B C . d I , ( A B C ) = 1 3 S ∆ A B C . 2 3 d ( M , ( A B C ) ) = 2 9 S ∆ A B C . d ( A ' , ( A B C ) )