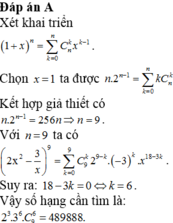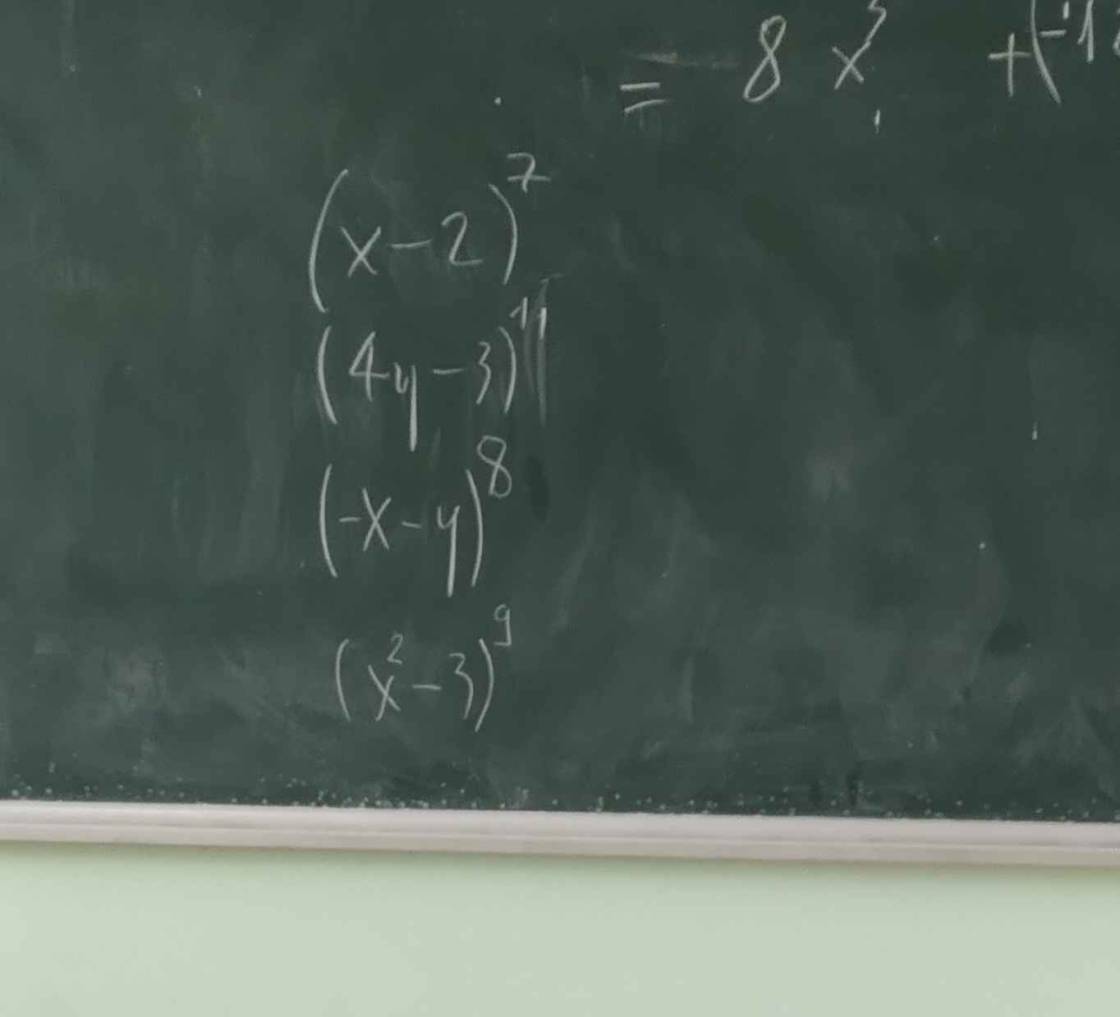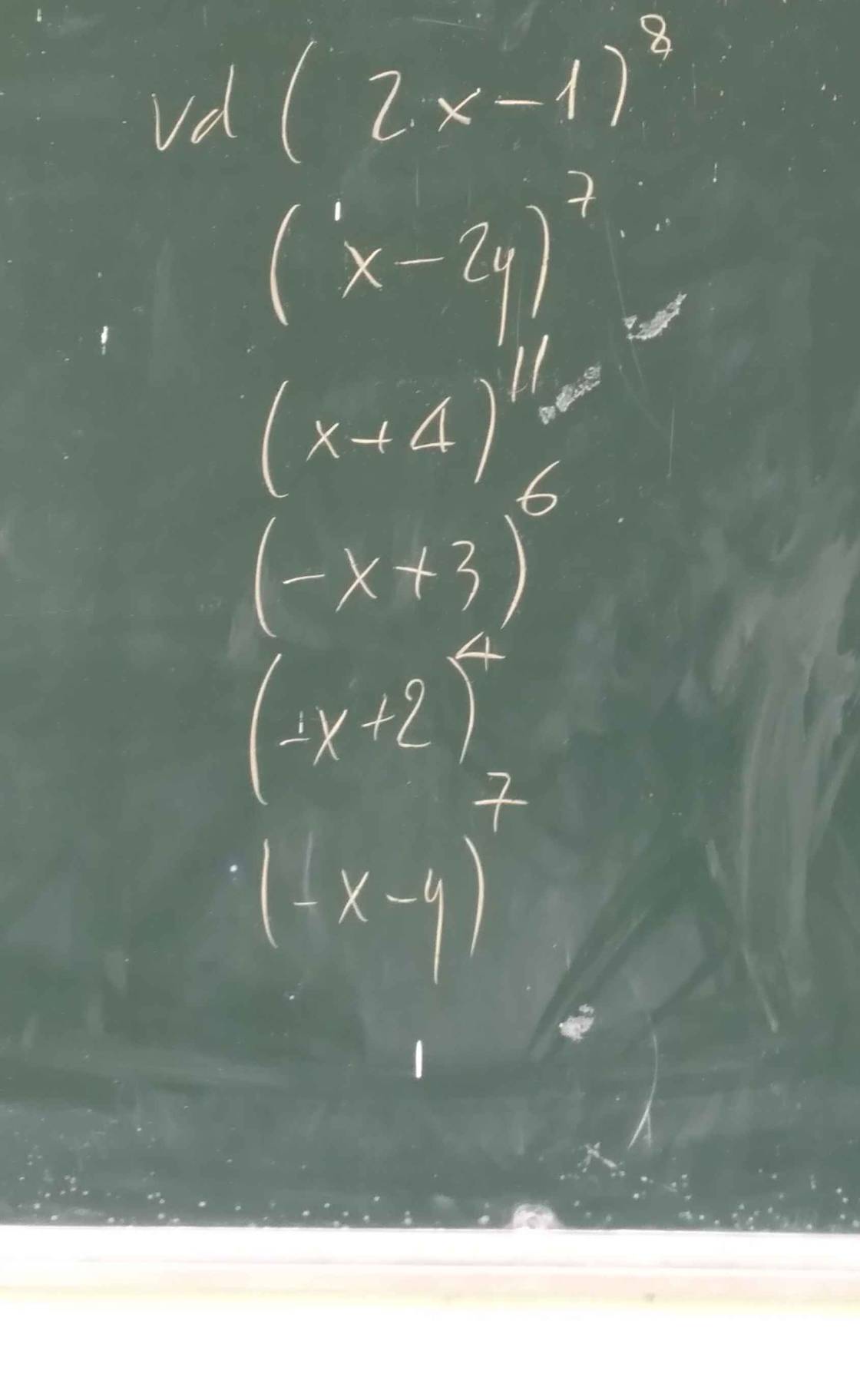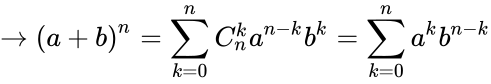Giúp với ạ nhị thức newton với hoán vị tổ hợp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
0
Những câu hỏi liên quan
DV
1
21 tháng 4 2023
a: (x-2)^7
\(=C^0_7\cdot x^7\cdot\left(-2\right)^0+C^1_7\cdot x^6\cdot\left(-2\right)^1+...+C^7_7\cdot x^0\cdot\left(-2\right)^7\)
\(=x^7-14x^6+84x^5-280x^4+560x^3-672x^2+448x-128\)
b: (4y-3)^11
\(=C^0_{11}\cdot\left(4y\right)^{11}\cdot\left(-3\right)^0+C^1_{11}\cdot\left(4y\right)^{10}\cdot\left(-3\right)^1+...+C^{11}_{11}\cdot\left(4y\right)^0\cdot\left(-3\right)^{11}\)
=
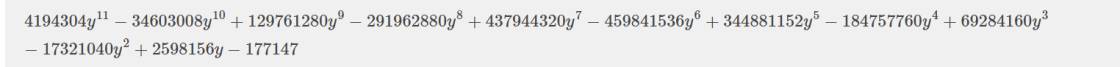
c: (-x-y)^8=(x+y)^8
=
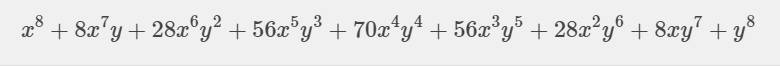
d: (x^2-3)^9
\(=C^0_9\cdot\left(x^2\right)^9\cdot\left(-3\right)^0+C^1_9\cdot\left(x^2\right)^8\cdot\left(-3\right)^1+...+C^9_9\cdot\left(x^2\right)^0\cdot\left(-3\right)^9\)
=
DV
1
28 tháng 4 2023
a: (2x-1)^8
\(=\sum_{k=0}^8C^k_8\cdot\left(2x\right)^k\cdot\left(-1\right)^{8-k}\)
=
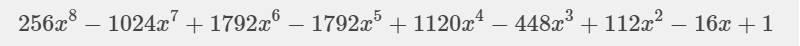
b: (x-2y)^7
\(=\sum_{k=0}^n\cdot C^k_7\cdot x^{7-k}\cdot\left(-2y\right)^k\)
=
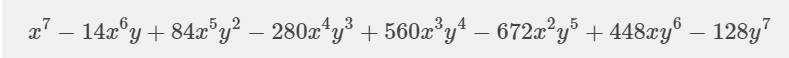c: (x+4)^11
\(=\sum_{k=0}^n\cdot C^k_{11}\cdot x^{11-k}\cdot4^k\)
=
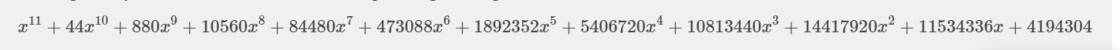
d: (-x+3)^6=(x-3)^6
\(=\sum_{k=0}^6\cdot x^{6-k}\cdot\left(-3\right)^k\)
e: (-x+2)^4=(x-2)^4
\(=\sum_{k=0}^4\cdot C^k_4\cdot x^{4-k}\cdot\left(-2\right)^k\)
=
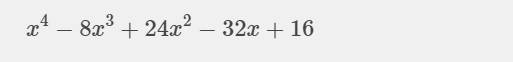
f: (-x-y)^7
\(=\sum_{k=0}^7\cdot C^k_7\cdot\left(-x\right)^{7-k}\cdot\left(-y\right)^k\)
=
KA
1
CT
10 tháng 11 2021
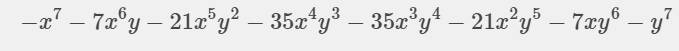
Tham khảo :
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a+b)n) thành một đa thức có n+1 số hạng.
HT
Công thức
NV
1
VQ
12 tháng 10 2021
n!=1.2.3...nn!=1.2.3...n. Quy ước: 0!=10!=1
n!=(n−1)!nn!=(n−1)!n
n!p!=(p+1)(p+2)....nn!p!=(p+1)(p+2)....n (với n>pn>p)
n!(n−p)!=(n−p+1)(n−p+2)....nn!(n−p)!=(n−p+1)(n−p+2)....n (với n>pn>p)
2. Hoán vị (không lặp)
Một tập hợp gồm n phần tử (n≥1)(n≥1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n phần tử.
Số hoán vị của n phần tử là Pn=n!Pn=n!
3. Hoán vị lặp
Cho k phần tử khác nhau a1;a2;...;aka1;a2;...;ak . Mỗi cách sắp xếp n phần tử trong đó gồm n1 phần tử a1; n2 phần tử a2;…; nk phần tử ak (n1+n2+...+nk=n)(n1+n2+...+nk=n) theo một thứ tự nào đó được gọi là một hoán vị lặp cấp n và kiểu (n1;n2;...;nk)(n1;n2;...;nk) của k phần tử
Số các hoán vị lặp cấp n kiểu (n1;n2;;;;nk)(n1;n2;;;;nk) của k phần tử là:
Pn(n1;n2;...;nk)=n!n1!n2!...nk!Pn(n1;n2;...;nk)=n!n1!n2!...nk!
HƯỚNG DẪN GIẢI
8 tháng 4 2019
\(x^8-1=\left(x^2-1\right)\left(x^4+x^2+1\right)\)
CÂU SAU THÌ MK KO BIẾT
