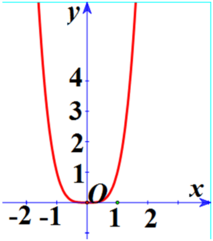
Giả sử hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ. Khi đó:
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Đồ thị hướng xuống và có 3 cực trị nên a < 0 , b > 0 suy ra câu A ( c không có điều kiện)

Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
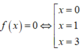
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
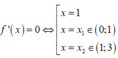
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
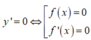
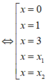
Ta có BXD của y' như sau
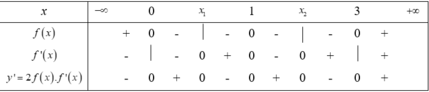
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.

Đáp án B
Ta thấy f ' x đổi dấu qua 1 điểm x 0 ⇒ hàm số có 1 cực trị
Chọn B.
Đồ thị hướng lên nên a > 0 . Có 1 cực trị nên a b ≥ 0 suy ra b ≥ 0 . Qua (0; 0) nên c = 0 . Do đó chọn câu B.