Cho hàm số y = x 4 + b x 2 + c có đồ thị (C). Chọn khẳng định đúng nhất:
A. Đồ thị (C) có ít nhất một điểm cực đại.
B. Đồ thị (C) có đúng một điểm cực tiểu.
C. Đồ thị (C) có ít nhất một điểm cực tiểu.
D. Đồ thị (C) có đúng một điểm cực đại.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số 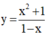 có đồ thị hàm số như sau:
có đồ thị hàm số như sau:
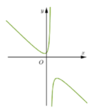 õ ràng
õ ràng ![]()
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số ![]() => Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là:
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: ![]() luôn song song với trục hoành.
luôn song song với trục hoành.
Vậy (III) đúng.

Đáp án A
Xét hệ phương trình
f ' ( x ) = 3 x 2 + 6 a x + 3 = 0 ( * ) g ' ( x ) = 3 x 2 + 6 b x + 9 = 0 ⇒ 6 x ( a − b ) = 6 ⇔ x = 1 a − b .
Áp dụng công thức nghiệm do phương trình (*) ta có x = − a ± a 2 − 1 với a ∈ ( − ∞ ; − 1 ) ∪ 1 ; + ∞ .
*Trường hợp 1: x = − a + a 2 − 1 .
Ta có
1 a − b = − a + a 2 − 1 ⇔ b = a + 1 a − a 2 − 1 = 2 a + a 2 − 1
Suy ra
P = a + 2 b = a + 4 a + 2 a 2 − 1 ≥ 5 a + 2 a 2 − 1
Xét hàm số
f ( x ) = 5 x + 2 x 2 − 1 ; x ∈ − ∞ ; − 1 ∪ 1 ; + ∞ .
Đạo hàm
f ' x = 5 + 2 x x 2 − 1 ; f ' x = 0 ⇔ 5 x 2 − 1 = − 2 x ⇔ x ≤ 0 25 x 2 − 1 = 4 x 2
⇔ x = − 5 21 (thỏa mãn).
Lại có f − 5 21 = − 21 ⇒ P ≥ 21 (lập bảng biến thiên của hàm số f x ).
*Trường hợp 2:Tương tự, ta tìm được P ≥ 21 .

Chọn C.
Từ đồ thị suy ra hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = ± 1 nên loại A, B, D

Chọn C.
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.


Chọn A
Ta có:
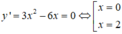
![]()
nên x = 0 là điểm cực đại của hàm số, yCĐ = 9.
Vậy điểm cực đại của đồ thị hàm số là M (0;9).
Chọn C.
Do a = 1 > 0 nên (C) có 2 trường hợp là có 1 điểm cực tiểu hay có 2 điểm cực tiểu và một điểm cực đại.