Cho hàm số f x = x 3 − 6 x 2 + 9 x . Đặt f k x = f f k − 1 x (với k là số tự nhiên lớn hơn 1). Tính số nghiệm của phương trình f 6 x = 0
A. 729
B. 365
C. 730
D. 364
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào đồ thị ta thấy phương trình ![]() chỉ có một nghiệm đơn và hai nghiệm kép nên
chỉ có một nghiệm đơn và hai nghiệm kép nên ![]() chỉ đổi dấu khi qua nghiệm đơn này.
chỉ đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số f(x) có đúng một cực trị.
Chọn A.

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
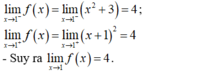
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
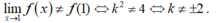
Chọn A

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.
Đáp án B
Ta có f x = x x − 3 2 ; f x = 0 ⇔ x = 0 x = 3 .
Gọi a k là số nghiệm của phương trình f k x = 0 và b k là số nghiệm của phương trình f k x = 3.
Khi đó a k = a k − 1 + b k − 1 b k = 3 k k ∈ ℕ * , k ≥ 2
suy ra a n = a n − 1 + 3 n − 1 → a n = a 1 + 3 n − 3 2 * .
Mà a 1 = 2 nên suy ra * ⇔ a n = 2 + 3 n − 3 2 = 3 n + 1 2 .
Với n = 6 ⇒ f 6 x = 0 có 3 6 + 1 2 = 365 nghiệm.