Cho a,b,c >0 thỏa mãn Giá trị lớn nhất của biểu thức đạt tại (x;y;z) Giá trị của là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Ta có : \(\left(\frac{1}{a}-\frac{1}{b}\right)^2\ge0\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\)
Tương tự : \(\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}\); \(\frac{1}{a^2}+\frac{1}{c^2}\ge\frac{2}{ac}\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\). Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=9\)
\(9\le3\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c = 1
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=7\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2.\frac{a+b+c}{abc}=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=49\)

Theo giả thiết: \(a+b+c=3\Rightarrow b+c=3-a\). Tương tự: a+b=3-a và c+a=3-b
Khi đó \(\frac{1}{a^2+b+c}+\frac{1}{b^2+c+a}+\frac{1}{c^2+a+b}=\frac{1}{a^2-a+3}+\frac{1}{b^2-b+3}+\frac{1}{c^2-c+3}\)
Ta chứng minh BĐT phụ sau:
\(\frac{1}{a^2-a+3}\le\frac{4-a}{9}\)(1)
Thật vậy, BĐT (1) \(\Leftrightarrow9\le\left(4-a\right)\left(a^2-a+3\right)\)
\(\Leftrightarrow9\le-a^3+5a^2-7a+12\)\(\Leftrightarrow-a^3+5a^2-7a+3\ge0\)
\(\Leftrightarrow-a^3+a^2+4a^2-4a-3a+3\ge0\)
\(\Leftrightarrow-a^2\left(a-1\right)+4a\left(a-1\right)-3\left(a-1\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)\left(-a^2+4a-3\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)\left(-a^2+a+3a-3\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)\left[-a\left(a-1\right)+3\left(a-1\right)\right]\ge0\)
\(\Leftrightarrow\left(a-1\right)^2\left(3-a\right)\ge0\)(2)
Ta thấy \(a;b;c>0\) và \(a+b+c=3\Rightarrow a< 3\)\(\Rightarrow3-a>0\)
Mà \(\left(a-1\right)^2\ge0\forall a\). Nên \(\left(a-1\right)^2\left(3-a\right)\ge0\)
Do đó: BĐT (2) luôn đúng với mọi 0<a<3 => BĐT (1) cũng đúng
Chứng minh tương tự \(\frac{1}{b^2-b+3}\le\frac{4-b}{9};\frac{1}{c^2-c+3}\le\frac{4-c}{9}\)
Từ đó suy ra:
\(\frac{1}{a^2-a+3}+\frac{1}{b^2-b+3}+\frac{1}{c^2-c+3}\le\frac{12-\left(a+b+c\right)}{9}=\frac{12-3}{9}=1\)(Do a+b+c=3)
=> ĐPCM.
Cho x,y,z € Z+ tm: x+y+z=4
Tính A= \(\sqrt{ }\)x(4-y)(4-z) +\(\sqrt{ }\)y(4-x)(4-x) +\(\sqrt{ }\)z(4-x)(4-y) -\(\sqrt{ }\)xyz

a) Bất phương trình đã cho tương đương với hệ sau:
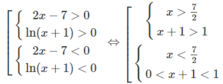
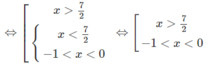
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
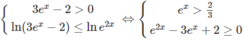
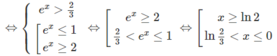
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )

gt <=> \(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=1\)
Đặt: \(\frac{1}{a}=x;\frac{1}{b}=y;\frac{1}{c}=z\)
=> Thay vào thì \(VT=\frac{\frac{1}{xy}}{\frac{1}{z}\left(1+\frac{1}{xy}\right)}+\frac{1}{\frac{yz}{\frac{1}{x}\left(1+\frac{1}{yz}\right)}}+\frac{1}{\frac{zx}{\frac{1}{y}\left(1+\frac{1}{zx}\right)}}\)
\(VT=\frac{z}{xy+1}+\frac{x}{yz+1}+\frac{y}{zx+1}=\frac{x^2}{xyz+x}+\frac{y^2}{xyz+y}+\frac{z^2}{xyz+z}\ge\frac{\left(x+y+z\right)^2}{x+y+z+3xyz}\)
Có BĐT x, y, z > 0 thì \(\left(x+y+z\right)\left(xy+yz+zx\right)\ge9xyz\)Ta thay \(xy+yz+zx=1\)vào
=> \(x+y+z\ge9xyz=>\frac{x+y+z}{3}\ge3xyz\)
=> Từ đây thì \(VT\ge\frac{\left(x+y+z\right)^2}{x+y+z+\frac{x+y+z}{3}}=\frac{3}{4}\left(x+y+z\right)\ge\frac{3}{4}.\sqrt{3\left(xy+yz+zx\right)}=\frac{3}{4}.\sqrt{3}=\frac{3\sqrt{3}}{4}\)
=> Ta có ĐPCM . "=" xảy ra <=> x=y=z <=> \(a=b=c=\sqrt{3}\)
Đáp án A