Không vẽ đồ thị, hãy giải thích vì sao các hệ phương trình có 1 nghiệm duy nhất 3 x = 6 2 y = - 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2018
3 x + 5 y = 15 2 y = - 7 ⇔ y = - 3 5 x + 3 x = - 3 , 5
Ta có đường thẳng y = -3,5 song song với trục hoành
Đường thẳng y = - 3 5 x + 3 cắt trục hoành nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất
PT
1
CM
11 tháng 2 2019
3 x = 6 x - 3 y = 2 ⇔ x = 2 y = 1 3 x - 2 3
Ta có đường thẳng x = 2 song song với trục tung. Đường thẳng y = 1 3 x - 2 3 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất.
CM
5 tháng 12 2019
Vì đường thẳng y = 3 song song với trục hoành còn đường thẳng y = - 23 8 x + 25 4 cắt hai trục tọa độ nên chúng cắt nhau.
Vậy hệ phương trình có một nghiệm duy nhất.
CM
13 tháng 4 2018
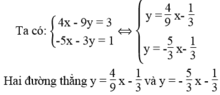
cắt nhau vì chúng có hệ số góc khác nhau.
Vậy hệ phương trình có một nghiệm duy nhất.
CM
26 tháng 7 2019
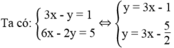
Vì hai đường thẳng có hệ số góc đều bằng 3 nhưng tung độ gốc khác nhau (-1 ≠ - 5/2 ) nên chúng song song với nhau.
Vậy hệ phương trình vô nghiệm.
CM
1 tháng 2 2019
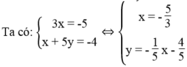
Vì đường thẳng x = - 5/3 song song với trục tung còn đường thẳng y = - 1 5 x - 4 5 cắt hai trục tọa độ nên chúng cắt nhau.Vậy hệ phương trình có một nghiệm duy nhất.
CM
27 tháng 2 2018
Ta có: I(-1,5; 4,5), J(1; 2)
*x = -1,5 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2 - 1 , 5 2 + (-1,5) – 3 = 4,5 – 4,5 = 0
*x = 1 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2. 1 2 + 1 – 3 = 3 – 3 = 0
CM
3 tháng 7 2019
Khi a và c trái dấu thì ac < 0, suy ra –ac > 0, suy ra -4ac > 0
Ta có: ∆ = b 2 – 4ac, trong đó b 2 > 0
Nếu -4ac > 0 thì ∆ luôn lớn hơn 0.
Khi ∆ > 0 nghĩa là phương trình có hai nghiệm phân biệt.
Áp dụng :
Phương trình 3 2 x 2 + 3 - 2 x + 2 - 3 = 0 có:
a = 3 2 , c = 2 - 3 nên ac < 0 (vì 2 < 3 )
Vậy phương trình có 2 nghiệm phân biệt.
3 x = 6 2 y = - 7
Đường thẳng 3x = 6 song song với trục tung. Đường thẳng 2y = -7 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất