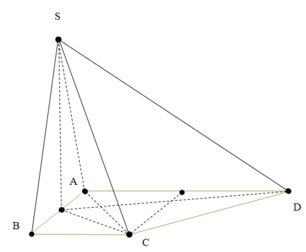
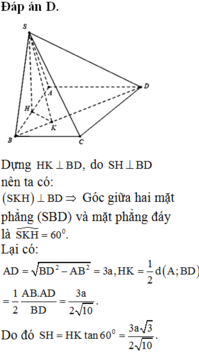
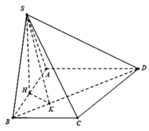
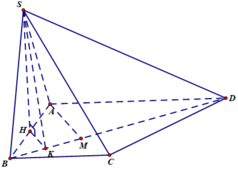
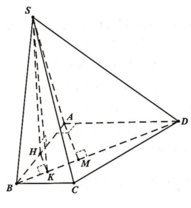
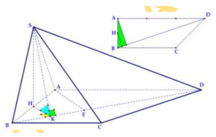
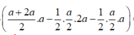Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB=a, BC=2a, BD=a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 0 . Tính thể tích V của khối chóp S.ABCD theo a.
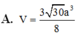
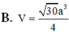
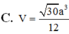
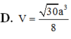

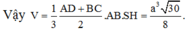
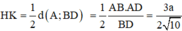

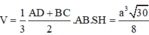
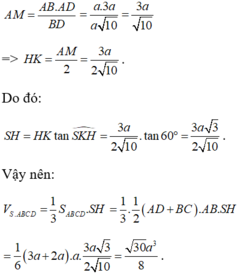

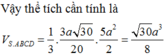

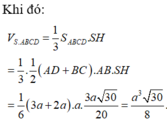
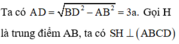
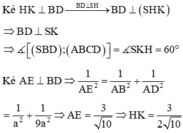


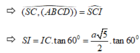 =
a
15
2
=
a
15
2