Cho cấp số cộng ( u n ) , n ∈ N * gồm các số dương. Xét biểu thức S = 1 u 1 + u 2 + 1 u 2 + u 3 + . . . + 1 u 2017 + u 2018 . Mệnh đề nào sau đây là đúng?
A. S = 2017 u 1 + u 2018
B. S = 2018 u 1 + u 2018
C. S = 1 2017 u 1 + u 2018
D. S = 1 2018 u 1 + u 2018

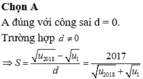
Đáp án A
đúng với công sai d = 0. Trường hợp d #0