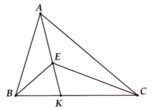
Cho tam giác ABC, E là một điểm bất kì nằm trong tam giác. Chứng minh rằng: BEC ^ = ABE ^ + ACE ^ + BAC ^ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
30 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 11 2019
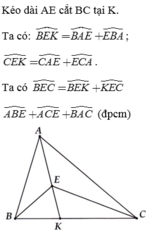
\(\widehat{BEC}=360-\left(\widehat{AEB}+\widehat{AEC}\right)\)
\(\widehat{AEB}=180-\left(\widehat{ABE}+\widehat{BAE}\right)\)
\(\widehat{AEC}=180-\left(\widehat{ACE}+\widehat{CAE}\right)\)
\(\widehat{BEC}=360-180+\left(\widehat{ABE}+\widehat{BAE}\right)-180+\left(\widehat{ACE}+\widehat{CAE}\right)=\)
\(=\widehat{ABE}+\widehat{ACE}+\left(\widehat{BAE}+\widehat{CAE}\right)=\widehat{ABE}+\widehat{ACE}+\widehat{BAC}\)
PT
14 tháng 11 2019
Mình làm theo cách của mình, bạn tham khảo :v
Trên hình, ta có giả thiết ( tổng ba góc 1 tam giác ): \(\widehat{BAC}=180^0-\left(\widehat{B}+\widehat{C}\right)\)
\(\widehat{ABE}=\widehat{ABC}-\widehat{EBC}\)
\(\widehat{ACE}=\widehat{ACB}-\widehat{ECB}\)
Ta có: \(\widehat{BAC}+\widehat{ABE}+\widehat{ACE}\Rightarrow\left[180^0-\left(\widehat{ABC}+\widehat{ACB}\right)\right]+\left(\widehat{ABC}-\widehat{EBC}\right)+\left(\widehat{ACB}-\widehat{ECB}\right)\)
Bỏ ngoặc, ta có:
\(180^0-\widehat{ABC}-\widehat{ACB}+\widehat{ABC}-\widehat{EBC}+\widehat{ACB}-\widehat{ECB}\)
\(\Rightarrow180^0-\widehat{EBC}-\widehat{ECB}=180^0-\left(\widehat{EBC}+\widehat{ECB}\right)\) ( Rút gọn biểu thức )
Mà \(180^0-\left(\widehat{EBC}+\widehat{ECB}\right)=\widehat{BEC}\) ( Tổng ba góc của 1 tam giác )
Vậy \(\widehat{BEC}=\widehat{ABE}+\widehat{ACE}+\widehat{BAC}\) ( dpcm )
ON
27 tháng 10 2017
Ta có tam giác ABC = 90 độ nên
\(\widehat{ABC}+\widehat{ACE}=90^0\)
Vì lấy điểm E nằm trong tam giác nên\(\widehat{ABE}+\widehat{EBC}+\widehat{ACE}+\widehat{ECB}=90^0\)
\(\Rightarrow\)\(\widehat{EBC}+\widehat{ECB}< 90^0\); \(\widehat{EBC}+\widehat{ECB}< 90^0\)
Nên \(\widehat{BEC}>90^0\)
TT
28 tháng 7 2015
Ta có tam giác ABC = 90 độ nên
góc ABC +góc ACB = 90 độ
vì lấy điểm E nằm trong tam giác nên
góc ABE + EBC + ACE + ECB = 90 độ
=> góc EBC + ECB < 90 độ
nên góc BEC > 90 độ