Cho ba lực đồng quy, cùng độ lớn F và cùng nằm trong một mặt phẳng. Biết góc tạo bởi các lưc F 1 → , F 2 → = F 3 → , F 4 → = 120 . Hợp lực của chúng bằng
A. 0.
B. F.
C. 2F.
D. 3F.
Chọn A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
![]()

Theo quy tắc hình bình hành và kết hợp với điều kiện ba lực F 1 → , F 2 → , F 3 → có độ lớn bằng nhau.
=> Hình bình hành thành hình thoi nên hợp lực của F 1 → và F 3 → cùng phương, cùng chiều với lực F 2 → nên độ lớn hợp lực của ba lực trên là:
![]()

Chọn A.
Hợp lực:
F = F 1 ⇀ + F 2 ⇀ + F 3 ⇀ = F - 13 + F 2 ⇀
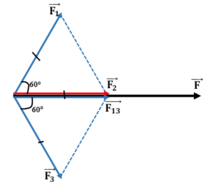

Chọn D.
![]()
Theo quy tắc hình bình hành (Hình vẽ):
![]()
![]()
Vì F2 = F3 => Đa giác OF2F23F3 là hình thoi nên
( F 23 → , F 2 → )= 60 °
⇒ F 23 → vuông góc với F 1 → vậy
![]()
vậy:

Chọn D.
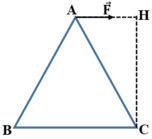
Cánh tay đòn của lực F ⇀ là CH. Do đó momen của lực F→ đối với trục quay đi qua C và vuông góc với mặt phẳng khung là:
M F / C = F.CH = F . l 3 / 2

Chọn D.
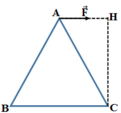
Cánh tay đòn của lực F → là CH. Do đó momen của lực F → đối với trục quay đi qua C và vuông góc với mặt phẳng khung là: MF/C = F.CH = Fℓ 3 /2.
Chọn A.
Áp dụng quy tắc hình bình hành xác định hợp lức (Hình vẽ):
F 12 → cùng phương, ngược chiều F 3 →
Nên hợp lực của ba lực là: F = |F – F12| = 0.