Tìm x:
a ) x - 1 2 = 2 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
2 tháng 11 2017
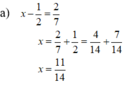
bài 1:
a) (x+1)^2-(x-1)^2-3(x+1)(x-1)
=(x+1+x-1)(x+1-x+1)-3x^2-3
=2x^2-3x^2-3
=-x^2-3
D2
2
3 tháng 10 2021
a) \(\Rightarrow x^2+8x+16-x^2+1=19\)
\(\Rightarrow8x=2\Rightarrow x=\dfrac{1}{4}\)
b) \(\Rightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)
\(\Rightarrow2x=-255\Rightarrow x=-\dfrac{255}{2}\)
3 tháng 10 2021
a: Ta có: \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=19\)
\(\Leftrightarrow x^2+8x+16-x^2+1=19\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
b: Ta có: \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)
\(\Leftrightarrow2x=-255\)
hay \(x=-\dfrac{255}{2}\)
NL
1.Tìm x,y để (x+1)(y^2-6)=0
2.Tìm x biết x^2-12x+7=7
3.Tìm giá trị nhỏ nhất của A=(x+2)^2+(Y-1/5)^2-10
0
20 tháng 12 2021
a: \(A=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x}{x^2+x+1}\)
KV
8 tháng 6 2023
a) Ta có:
1; 4; 7;...; 100 có (100 - 1) : 3 + 1 = 34 (số)
1 + 4 + 7+ ... + 100 = (100 + 1) × 34 : 2
= 101 × 17
(1 + 4 + 7 + ... + 100) : a = 17
101 × 17 : a = 17
a = 101 × 17 : 17
a = 100
b) (X - 1/2) × 5/3 = 7/4 - 1/2
(X - 1/2) × 5/3 = 5/4
X - 1/2 = 5/4 : 5/3
X - 1/2 = 3/4
X = 3/4 + 1/2
X = 5/4
LM
Lê Minh Vũ
CTVHS
8 tháng 6 2023
a) (1 + 4 + 7 +...+ 100) : a = 17
1717 : a = 17
a = 101
b) \(\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{7}{4}-\dfrac{1}{2}\)
\(\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{10}{8}\)
\(\left(x-\dfrac{1}{2}\right)=\dfrac{10}{8}\div\dfrac{5}{3}\)
\(\left(x-\dfrac{1}{2}\right)=\dfrac{10}{8}\times\dfrac{3}{5}\)
\(\left(x-\dfrac{1}{2}\right)=\dfrac{3}{4}\)
\(x-\dfrac{1}{2}=\dfrac{3}{4}\)
\(x=\dfrac{3}{4}+\dfrac{1}{2}\)
\(x=\dfrac{5}{4}\)
LM
Lê Minh Vũ
CTVHS
7 tháng 8 2023
Bài 1:
a) \(\dfrac{9}{20}-\dfrac{8}{15}\times\dfrac{5}{12}\)
\(=\dfrac{9}{20}-\dfrac{2}{9}\)
\(=\dfrac{41}{180}\)
b) \(\dfrac{2}{3}\div\dfrac{4}{5}\div\dfrac{7}{12}\)
\(=\dfrac{2}{3}\times\dfrac{5}{4}\times\dfrac{12}{7}\)
\(=\dfrac{5}{6}\times\dfrac{12}{7}\)
\(=\dfrac{10}{7}\)
c) \(\dfrac{7}{9}\times\dfrac{1}{3}+\dfrac{7}{9}\times\dfrac{2}{3}\)
\(=\dfrac{7}{9}\times\left(\dfrac{1}{3}+\dfrac{2}{3}\right)\)
\(=\dfrac{7}{9}\times1\)
\(=\dfrac{7}{9}\)
LM
Lê Minh Vũ
CTVHS
7 tháng 8 2023
Bài 2:
a) \(2\times\left(x-1\right)=4026\)
\(\left(x-1\right)=4026\div2\)
\(x-1=2013\)
\(x=2014\)
Vậy: \(x=2014\)
b) \(x\times3,7+6,3\times x=320\)
\(x\times\left(3,7+6,3\right)=320\)
\(x\times10=320\)
\(x=320\div10\)
\(x=32\)
Vậy: \(x=32\)
c) \(0,25\times3< 3< 1,02\)
\(\Leftrightarrow0,75< 3< 1,02\) ( S )
=> \(0,75< 1,02< 3\)
TH
2
21 tháng 8 2021
Ta có: \(A=\left(1+\dfrac{2}{3}\right)\cdot\left(1+\dfrac{2}{5}\right)\cdot\left(1+\dfrac{2}{7}\right)\cdot...\cdot\left(1+\dfrac{2}{2021}\right)\)
\(=\dfrac{5}{3}\cdot\dfrac{7}{5}\cdot\dfrac{9}{7}\cdot...\cdot\dfrac{2023}{2021}\)
\(=\dfrac{2023}{3}\)
TN
20 tháng 7 2018
\(-2.\left(x+\frac{1}{3}\right)-5.\left(x+\frac{1}{3}\right)=\frac{1}{2}.x\) \(x\)
<=> \(\left(x+\frac{1}{3}\right).\left(-2-5\right)=\frac{1}{2}.x\)
<=> \(\left(x+\frac{1}{3}\right).\left(-7\right)=\frac{1}{2}.x\)
<=> \(-7x-\frac{7}{3}=\frac{1}{2}.x\)
<=> \(-7x-\frac{1}{2}.x=\frac{7}{3}\)
<=> \(\left(-7-\frac{1}{2}\right).x=\frac{7}{3}\)
<=> \(\frac{-15}{2}.x=\frac{7}{3}\)
<=> \(x=\frac{7}{3}:\frac{-15}{2}=\frac{-14}{45}\)
\(-7x-\frac{7}{3}=\frac{1}{2}.x\)
<=> \(-7x-\frac{1}{2}x=\frac{7}{3}\)
<=> \(\left(-7-\frac{1}{2}\right).x=\frac{7}{3}\)
<=> \(\frac{-15}{2}.x=\frac{7}{3}\)
<=> \(x=\frac{7}{3}:\frac{-15}{2}=\frac{-14}{45}\)