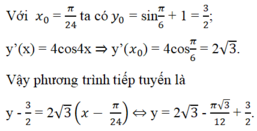Tập nghiệm của phương trình -9sinx+6cosx-3sin2x+cos2x= -10 là: x = a π b + k 2 π ( k ∈ Z ) tính giá trị của a2 – b : (biết a, b tối giản)
A.3
B.-2
C.4
D.-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

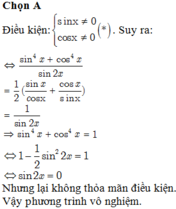

Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.

Đáp án B
Đặt t = 2 sin x 2 ≥ t ≥ 0 dựa vào đường tròn lượng giác ta thấy:
Với t ∈ 0 ; 2 một giá trị của t có 6 giá trị của x
Với t = 2 một giá trị của t có 3 giá trị của x
Với t = 0 một giá trị của t có 4 giá trị của x
Dựa vào đồ thị ta thấy rằng PT f 2 sin x = f m có 12 nghiệm phân biệt ⇔ P T : f t = f m
có 2 nghiệm phân biệt thuộc khoảng 0 ; 2 ⇔ f m ∈ − 27 16 ; 0 ⇔ m ∈ 0 ; 2 ⇒ T = 4

Chọn D
ta có cos2x - √3sin2x= 1
⇔ 1 2 cos 2x - 3 2 . sin 2 x = 1 2 ⇔ sin π 6 . c os2x - cos π 6 . sin2x = 1 2 ⇔ sin π 6 − 2 x = sin π 6 ⇔ π 6 − 2 x = π 6 + k 2 π π 6 − 2 x = π − π 6 + k 2 π ⇔ x = − k π x = − π 3 − k π ⇔ x = l π x = − π 3 + l π ( l = − k ∈ Z )
Suy ra phương trình chỉ có một nghiệm thuộc(0;π) là x = 2 π 3

Thấy : \(cos\) \(2x=1-2sin^2\left(x\right)\)
\(sin2x=2sinx.cosx\)
Thay vào ta được :
9 sinx + 6cosx - 6. sinx.cosx +1 -2.sin^2(x) -8 =0
9. (sinx-1) + 6.cosx. (1-sinx) +2 -2.sin^2(x) =0
9.(sinx-1) + 6cosx.(1-sinx) +2. (1-sinx) (1+sinx) =0
* TH1 : sinx=1 -> x =.....
* TH2 : sinx khác 1
Chia cả 2 vế cho sinx-1 ta được :
9 - 6.cosx -2 (1+sinx) =0
<--> 7 -6cosx - 2.sinx = 0
<--> 7- 4.cosx -2. (sinx+cosx)= 0
<-->7 - 4.cosx -2.căn2. sin(x+45) = 0 (1)
ta thấy Vế trái luôn > 0 với mọi x nên (1) vô nghiệm
Kết luận : sinx=1

a) Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.
Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.
Vì hàm số y = sin4x là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.
Các hàm số y = sin4x (C1) và y = sin4x + 1 (C2) có đồ thị như trên hình 1 và hình 2.
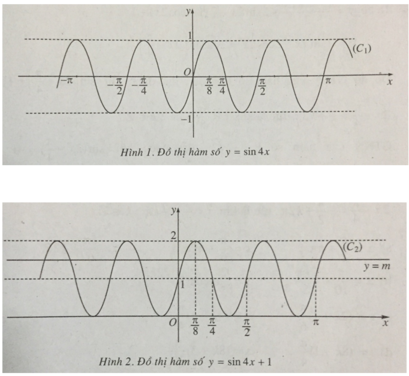
b) Vì sin4x + 1 = m ⇔ sin4x = m – 1
và -1 ≤ sin4x ≤ 1
nên -1 ≤ m – 1 ≤ 1
⇔ 0 ≤ m ≤ 2.
Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.
c) Phương trình tiếp tuyến của (C2) có dạng
y - y o = y ’ ( x o ) ( x - x o ) .