Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
Phương pháp
Tính xác suất theo phương pháp biến cố đối: “Không có cầu thủ nào sút vào”.
Cách giải:
Gọi A là biến cố: “Ít nhất một cầu thủ sút vào”.
Khi đó A ¯ là biến cố: “Không có cầu thủ nào sút vào”.
Gọi A là biến cố cầu thủ thứ nhất ghi bàn
B là biến cố cầu thủ thứ hai ghi bàn
X là biến cố ít nhất 1 trong hai cầu thủ ghi bàn
Suy ra: X ¯ = A ¯ . B ¯
Vì hai biến cố A ¯ ; B ¯ độc lập với nhau nên ta có:
P ( X ¯ ) = P ( A ¯ ) . P ( B ¯ ) = ( 1 − 0 , 8 ) . ( 1 − 0 , 7 ) = 0 , 06
Do đó, xác suất để có ít nhất 1 trong hai cầu thủ ghi bàn là:
P ( X ) = 1 − P ( X ¯ ) = 1 − 0 , 06 = 0 , 94
Chọn đáp án B
CÓ ÍT NHẤT 1 cầu thủ ghi bàn có 2 cách làm
cách thứ nhất:
có ít nhất 1 cầu thủ ghi bàn có 3 trường hợp xảy ra là: cầu thủ 1 ghi bàn cầu thủ 2 không ghi bàn, cầu thủ 2 ghi bàn cầu thủ 1 không ghi bàn, và cả 2 cầu thủ ghi bàn
suy ra sx bằng: 0.8.0,3+0,7.0,2+0,7.,8
cách thứ 2 là : sử dụng biến cố đối
A: không có cầu thủ nào ghi bàn
với P(A)=0,2.0,3
B" có ít nhất 1 cầu thủ ghi bàn"
P(B)=1-P(A)=1-0,2.0,3
Chọn đáp án A
Gọi Ai là biến cố “cầu thủ thứ I ghi bàn” với i ∈ 1 ; 2 ; 3 .
Các biến cố Ai độc lập với nhau và P(A1) = x; P(A2) = y; P(A3) = 0,6.
* Gọi A là biến cố “Có ít nhất một trong ba cầu thủ ghi bàn” P(A) = 0,976.
Ta có là biến cố “không có cầu thủ nào ghi bàn”.
Ta có phương trình
* Gọi B là biến cố “Cả ba cầu thủ đều ghi bàn” P(B) = 0,336.
Mặt khác P(B) = P(A1).P(A2).P(A3) = 0,6xy.
Ta có phương trình
* Từ (1) và (2) ta có hệ phương trình
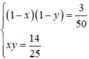
Suy ra x, y là nghiệm của phương trình
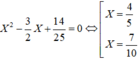
Do x > y nên x = 4 5 = 0 , 8 và y = 7 10 = 0 , 7 .
* Gọi C là biến cố “Có đúng hai cầu thủ ghi bàn”
Khi đó
⇒ P C = 0 , 452
\(Xác\text{ }suất\text{ }ít\text{ }nhất\text{ }để\text{ }một\text{ }trong\text{ }ba\text{ }cầu\text{ }thủ\text{ }gi\text{ }bàn\text{ }là:\)
\(1-\left(1-x\right)\left(1-y\right)\cdot0,4=0,976_{\left(1\right)}\)
\(Xác\text{ }suất\text{ }để\text{ }cả\text{ }ba\text{ }cầu\text{ }thủ\text{ }đều\text{ }ghi\text{ }bàn\text{ }là:\)
\(0,6xy=0,336\Leftrightarrow xy=56\Leftrightarrow y=\dfrac{0,56}{x}_{\left(2\right)}\)
\(Thay_{\left(2\right)}vào_{\left(1\right)}ta\text{ }có:\)
\(1-\left(1-x\right)\left(1-\dfrac{0,56}{x}\right)\cdot0,4=0,976\)
\(\Leftrightarrow\left(1-\dfrac{0,56}{x}-x+0,56\right)\cdot0,4=0,24\)
\(\Leftrightarrow1,56-\dfrac{0,56}{x}-x=0,06\)
\(\Leftrightarrow\dfrac{0,56}{x}+x=1,5\Leftrightarrow x^2-1,5x+0,56=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0,7\Rightarrow y=0,8\left(ktm\right)\\x=0,8\Rightarrow y=7\left(tm\right)\end{matrix}\right.\)
\(Xác\text{ }suất\text{ }để\text{ }có\text{ }đúng\text{ }hai\text{ }cầu\text{ }thủ\text{ }ghi\text{ }bàn\text{ }là:\\ 0,8\cdot0,7\cdot0,4+0,8\cdot0,3\cdot0,6+0,2\cdot0,7\cdot0,6=0,452\)
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .
