Tìm x:
x - 1 2 = 2 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
MN
0
MN
0
MN
0
NL
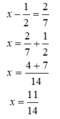
1.Tìm x,y để (x+1)(y^2-6)=0
2.Tìm x biết x^2-12x+7=7
3.Tìm giá trị nhỏ nhất của A=(x+2)^2+(Y-1/5)^2-10
0
ND
3
MN
6 tháng 7 2021
a) \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=16\)
(x + 4)2 - (x + 1) (x - 1) = 16
<=> (x2 + 8x + 16) - (x2 - 1) = 16
<=> x2 + 8x + 16 - x2 + 1 = 16
<=> 8x + 17 = 16
<=> 8x = -1
<=> x = −\(\dfrac{1}{8}\)
MN
6 tháng 7 2021
\(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)
\(4x^2+1-4x+\left(x^2+9+6x\right)-5\left(x^2-7^2\right)=0\)
\(4x^2+1-4x+x^2+9+6x-5x^2+245=0\)
\(\left(4x^2+x^2-5x^2\right)-\left(4x+6x\right)+\left(1+9+245\right)=0\)
\(2x+255=0\)
\(2x=-255\)
\(x=\dfrac{-255}{2}\)
P/s: Nhớ tick cho mình nha. Thanks bạn
18 tháng 2 2020
Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
28 tháng 2 2021
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)
13 tháng 7 2023
a: =>7/9:x=1/18-2/9=1/18-4/18=-3/18=-1/6
=>x=-7/9:1/6=-7/9*6=-42/9=-14/3
b: =>x*7/5=2/15+2/5=8/15
=>x=8/15:7/5=8/21
c: =>x-1/2=3/14:4/7=3/8
=>x=3/8+4/8=7/8
d: =>0,4x+0,3x-0,2x=0,7
=>0,5x=0,7
=>x=1,4
2 tháng 11 2017
bài 1:
a) (x+1)^2-(x-1)^2-3(x+1)(x-1)
=(x+1+x-1)(x+1-x+1)-3x^2-3
=2x^2-3x^2-3
=-x^2-3
D2
2
3 tháng 10 2021
a) \(\Rightarrow x^2+8x+16-x^2+1=19\)
\(\Rightarrow8x=2\Rightarrow x=\dfrac{1}{4}\)
b) \(\Rightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)
\(\Rightarrow2x=-255\Rightarrow x=-\dfrac{255}{2}\)
3 tháng 10 2021
a: Ta có: \(\left(x+4\right)^2-\left(x+1\right)\left(x-1\right)=19\)
\(\Leftrightarrow x^2+8x+16-x^2+1=19\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
b: Ta có: \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x+7\right)\left(x-7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5x^2+245=0\)
\(\Leftrightarrow2x=-255\)
hay \(x=-\dfrac{255}{2}\)
T
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 8 2023
\(\left(5-x\right)\left(x-2\right)+\left(x-7\right)\left(x+7\right)=\left(3x-1\right)^2-\left(3x-2\right)\left(3x+2\right)\\ \Leftrightarrow-x^2+7x-10+x^2-49=9x^2-6x+1-9x^2+4\\\Leftrightarrow7x-59=-6x+5\\ \Leftrightarrow13x=44\\ \Leftrightarrow x=\dfrac{64}{13} \)