Tìm tập nghiệm của các bất phương trình sau: x + x < 2 x + 3 x - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
PT
1
CM
14 tháng 4 2018
Ta có: x + x < ( 2 x + 3 ) ( x - 1 )
Điều kiện: x ≥ 0
⇔ x + x < 2 x - 2 x + 3 x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: x > 3
PT
1
CM
24 tháng 6 2018
Ta có: x − 3 x − 2 ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là x − 3 ≥ 0 x − 2 = 0 ⇔ x ≥ 3 x = 2
Vậy tập nghiệm của bất phương trình là S = { 2 } ∪ [3;+ ∞ )
PT
1
CM
10 tháng 8 2019
Ta có: ( x - 3 ) ( x - 2 ) ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là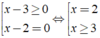
Vậy tập nghiệm của bất phương trình là x = 2 hoặc x ≥ 3
PT
1
NK
31 tháng 3 2020
a)11x-7<8x+7
<-->11x-8x<7+7
<-->3x<14
<--->x<14/3 mà x nguyên dương
---->x \(\in\){0;1;2;3;4}
NK
31 tháng 3 2020
b)x^2+2x+8/2-x^2-x+1>x^2-x+1/3-x+1/4
<-->6x^2+12x+48-2x^2+2x-2>4x^2-4x+4-3x-3(bo mau)
<--->6x^2+12x-2x^2+2x-4x^2+4x+3x>4-3+2-48
<--->21x>-45
--->x>-45/21=-15/7 mà x nguyên âm
----->x \(\in\){-1;-2}
24 tháng 2 2022
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Ta có: x + x < ( 2 x + 3 ) ( x - 1 )
Điều kiện: x ≥ 0
⇔ x + x < 2 x - 2 x + 3 x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: x > 3
Vậy bất phương trình đã cho có tập nghiệm là x > 3