Trong không gian Oxyz, cho ba điểm A, B, C lần lượt thuộc các tia
O
x
,
O
y
,
O
z
(không trùng với gốc tọa độ) sao cho
O
A
=
a
,
O
B
=
b
,
O
C
=
c
.
Giả sử M là một điểm thuộc miền trong của tam giác ABC và có khoảng cách đến các mặt
O
B
C
,
O
C
A
,
O
A
B
lần lượt...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A, B, C lần lượt thuộc các tia O x , O y , O z (không trùng với gốc tọa độ) sao cho O A = a , O B = b , O C = c . Giả sử M là một điểm thuộc miền trong của tam giác ABC và có khoảng cách đến các mặt O B C , O C A , O A B lần lượt là 1, 2, 3. Tính tổng S = a + b + c khi thể tích của khối chóp O . A B C đạt giá trị nhỏ nhất
A. S = 18
B. S = 9
C. S = 6
D. S = 24
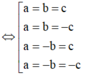
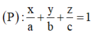
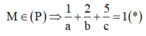
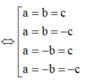
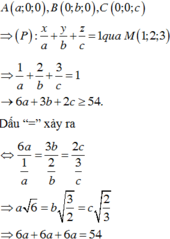
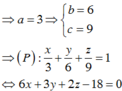
Đáp án A
Dễ dàng suy ra:
A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , a , b , c > 0
vì d M ; O B C = d M ; O y z = x M = 1 , tương tự ta có được M 1 ; 2 ; 3
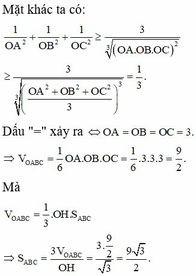
M ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 1.2.3 a . b . c 3 ⇔ a b c 6 = V O . A B C ≥ 27
Dấu bằng xảy ra khi:
1 a = 2 b = 3 c = 1 3 ⇒ a = 3 ; b = 6 ; c = 9 ⇒ a + b + c = 18