Mảnh bìa nào dưới đây có thể ghép được thành một hình lập phương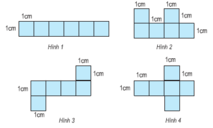
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PT
1
Những câu hỏi liên quan
PT
1
CM
5 tháng 7 2019
Cách 1: học sinh vẽ hình lên giấy rồi gấp thử và trả lời
Cách 2: suy luận:
-đương nhiên là không thể gấp hình 1 thành một hình lập phương.
- Với hình 2, khi ta gấp dãy 4 hình vuông ở dưới thành 4 mặt xung quanh thì 2 hình vuông ở trên sẽ đè lên nhau, không tạo thành một mặt đáy trên và một mặt đáy dưới được. Do đó hình 2 cũng bị loại.
- Hình 3 và hình 4 đều có thể gấp thành hình lập phương vì khi ta gấp dãy 4 hình vuông ở giữa thành 4 mặt xung quanh thì 2 hình vuông trên và dưới sẽ tạo thành hai mặt đáy trên và đáy dưới
Mỗi mảnh bìa ở hình 3 và hình 4 đều có thể gấp thành một hình lập phương.
Nói thêm :
a) Mọi mảnh bìa (6 hình vuông bằng nhau) gồm có một dãy 4 hình vuông ở giữa, 1 hình vuông ở phía trên, 1 hình vuông ở phía dưới đều có thể gấp lại thành một hình lập phương.
Ví dụ, các mảnh bìa sau có thể gấp được thành hình lập phương:
b) Mọi mảnh bìa gồm 6 hình vuông bằng nhau nhưng không có dạng đã nêu ở (a) thì không thể gấp lại thành hình lập phương được.
SJ
1
6 tháng 8 2015
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương.
3 tháng 12 2017
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương.
DL
25 tháng 11 2015
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương. hi hi tick nhé
SK
3 tháng 12 2017
Ta có : \(333^{333}=\left(333^4\right)^{83}\cdot333=\left(...1\right)^{83}\cdot333=\left(...1\right)\cdot333=\left(...3\right)\)
\(555^{555}=\left(...5\right)\)
\(777^{777}=\left(777^4\right)^{194}\cdot777=\left(...1\right)^{194}\cdot777=\left(...1\right)\cdot777=\left(...7\right)\)
18 tháng 3 2018
Để mình giải giúp bạn nha!!!
Hình như bạn vừa trả lời câu này thì phải: http://vn.answers.yahoo.com/question/ind...
Cũng tương tự như mình vừa chứng minh câu trên.
Giờ ta phải chứng minh cho 1 số chính phương chia cho 3 chỉ dư 0 hoặc 1
Với số tự nhiên a có dạng a=3k±1
=> a²=(3k±1)²=9k²±6k+1 chia cho 3 dư 1
Với a⁞3 thì chắc chắn a² chia cho 3 dư 0 rồi.
Xong.
Việc còn lại của bạn bây giờ quá đơn giản, chứng minh cho số đó chia cho 3 dư 2.
Nếu 1000 mảnh bìa đó xếp thành 1 số thì nó se có tổng các chữ số là:
(2+1001)x1000/2 = 501500 chia cho 3 dư 2. Vậy số ta vừa ghép được chia cho 3 dư 2.
=> số đó không phải số chính phương.
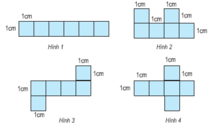
Cách 1: học sinh vẽ hình lên giấy rồi gấp thử và trả lời
Cách 2: suy luận:
-đương nhiên là không thể gấp hình 1 thành một hình lập phương.
- Với hình 2, khi ta gấp dãy 4 hình vuông ở dưới thành 4 mặt xung quanh thì 2 hình vuông ở trên sẽ đè lên nhau, không tạo thành một mặt đáy trên và một mặt đáy dưới được. Do đó hình 2 cũng bị loại.
- Hình 3 và hình 4 đều có thể gấp thành hình lập phương vì khi ta gấp dãy 4 hình vuông ở giữa thành 4 mặt xung quanh thì 2 hình vuông trên và dưới sẽ tạo thành hai mặt đáy trên và đáy dưới
Mỗi mảnh bìa ở hình 3 và hình 4 đều có thể gấp thành một hình lập phương.
Nói thêm :
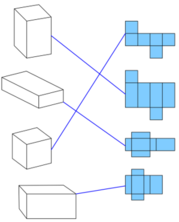
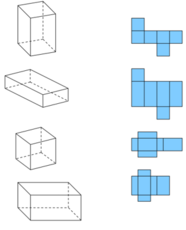
a) Mọi mảnh bìa (6 hình vuông bằng nhau) gồm có một dãy 4 hình vuông ở giữa, 1 hình vuông ở phía trên, 1 hình vuông ở phía dưới đều có thể gấp lại thành một hình lập phương.
Ví dụ, các mảnh bìa sau có thể gấp được thành hình lập phương:
b) Mọi mảnh bìa gồm 6 hình vuông bằng nhau nhưng không có dạng đã nêu ở (a) thì không thể gấp lại thành hình lập phương được.