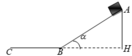
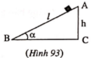
: Mặt phẳng nghiêng hợp với phương ngang một góc α = 30 0 , tiếp theo là mặt phẳng nằm ngang như hình vẽ. một vật trượt không vận tốc ban đầu từ đỉnh A của mặt phăng nghiêng với độ cao h=1m và sau đó tiếp tục trượt trên mặt phẳng nằn ngang một khoảng là BC. Tính BC, biết hệ số ma sát giữa vật với hai mặt phẳng đều là μ = 0 , 1

Chọn mốc thế năng tại mặt nằm ngang BC
Theo định luật bảo toàn năng lượng
W A = W C + A m s
Mà W A = m g . A H = m .10 = 10. m ( J ) ; W C = 0 ( J ) A m s = μ m g cos α . A B + μ m g . B C = 0 , 1. m .10. cos 30 0 . A H sin 30 0 + 0 , 1. m .10. B C ⇒ A m s = m . 3 . + m . B C ⇒ 10. m = 0 + m 3 + m . B C ⇒ B C = 8 , 268 ( m )