Tìm số tự nhiên n, biết : - 3 n 81 = - 27
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

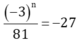
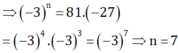

\(27^n.9^n=9^{27}:81\)
\(3^{3n}.3^{2n}=3^{54}:3^4\)
\(3^{5n}=3^{50}\)
=> 5n = 50
=> n = 10

\(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27.81
=> (-3)n = -(27.81)
=> (-3)n = -(33.34)
=> (-3)n = -37 = (-3)7
=> n = 7
Vậy n = 7
\(\frac{\left(-3\right)^n}{81}=-27\)
\(\left(-3\right)^n:81=-27\)
\(\left(-3\right)^n=-27\cdot81\)
\(\left(-3\right)^n=-2187\)
\(\left(-3\right)^n=\left(-3\right)^7\)
\(=>n=7\)

\(\frac{\left(-3\right)^n}{81}=-27\)
\(\left(-3\right)^n=-2187=\left(-3\right)^7\)
=> n = 7

mk ghi lại đề nha:
27n : 9n = 927 : 81
(27 : 9)n = 927 : 92
\(\Rightarrow\) 3n = 925
\(\Rightarrow\) 3n = (32)25
\(\Rightarrow\) 3n = 350
Vậy n = 50
\(27^n.9^n=9^{27}:81\Rightarrow3^{3n}:3^{2n}=3^{54}:3^4=3^{50}\)
\(\Rightarrow3^{5n}=3^{50}\Rightarrow5n=50\Rightarrow n=\frac{50}{5}=10\)

\(a,\frac{16}{2^n}=2=>\frac{2^4}{2^n}=2=>2^4:2^n=2=>2^{4-n}=2=>4-n=1=>n=3\)
\(b,\frac{\left(-3\right)^n}{81}=-27=>\frac{\left(-3\right)^n}{3^4}=\left(-3\right)^3=>\frac{\left(-3\right)^n}{\left(-3\right)^4}=\left(-3\right)^3=>\left(-3\right)^{n-4}=\left(-3\right)^3=>n-4=3=>n=7\)
\(c,8^n:2^n=4=>\left(8:2\right)^n=4=>4^n=4=>n=1\)

a) \(\frac{16}{2^n}=2\)
=> 2.2n = 16
=> 21+n = 24
=> 1 + n = 4
=> n = 4 - 1
=> n = 3
Vậy n = 3
b) \(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27.81
=> (-3)n = -33.34
=> (-3)n = (-3)7
=> n = 7
Vậy n = 7
c) 8n : 2n = 4
=> (8 : 2)n = 4
=> 4n = 41
=> n = 1
Vậy n = 1

\(\frac{16}{2^n}=2\Rightarrow2^n=16:2\Rightarrow2^n=8\Rightarrow n=3\)
\(\frac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=\left(-27\right).81\Rightarrow\left(-3\right)^n=-2187\Rightarrow n=7\)
\(8^n:2^n=4\Rightarrow\left(8:2\right)^n=4\Rightarrow4^n=4\Rightarrow n=1\)
a) => 2n = 16/2 = 8
=> n = 3
b) => (-3)n = -27 x 81 = -2187
=> n = 7
c) 8n : 2n = ( 8 : 2)n = 4n = 4
=> n = 1
