5. cho hình bình hành ABCD, có M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng BM=DN
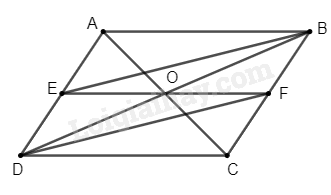
6. Cho hình bình hành ABCD, gọi E,F lần lượt là trung điểm của AB,CD.
a) Chứng minh rằng: Tứ giác DEBF là hình bình hành
b) DE cắt AC tại G, BF cắt AC tại H. Chứng minh: DE = EF = FB
7. Cho hình bình hành ABCD, kẻ AM vuông góc với BD tại H, kẻ CN vuông góc với BD tại k.
a) chứng minh rằng: tứ giác AMCN là hình bình hành
b) Gọi I là trung điểm của MN. Chứng minh rằng: ba điểm A,I,C thẳng hàng

5. Vì tứ giác ABCD là hình bình hành (gt)
=> AD // BC ; AD = BC (tc)
Vì M là trung điểm AD (gt)
N là trung điểm BC (gt)
AD = BC (cmt)
=> AM = DM = BN = CN
Vì AD // BC mà M ∈ AD, N ∈ BC
=> MD // BN
Xét tứ giác MBND có : MD = BN (cmt)
MD // BN (cmt)
=> Tứ giác MBND là hình bình hành (DHNB)
=> BM = DN (tc hình bình hành)
6. Vì tứ giác ABCD là hình bình hành (gt)
=> AB // CD ; AB = CD (tc)
Vì E là trung điểm AB (gt)
F là trung điểm CD (gt)
AB = CD (cmt)
=> AE = BE = DF = DF
Vì AB // CD mà E ∈ AB, F ∈ CD
=> BE // DF
Xét tứ giác DEBF có : BE = DF (cmt)
BE // DF (cmt)
=> Tứ giác DEBF là hình bình hành (DHNB)