Tính tổng tất cả các nghiệm của phương trình e sin x - π 4 = tan x thuộc đoạn 0 ; 50 π ?
A. 1853 π 2
B. 2475 π 2
C. 2671 π 2
D. 2105 π 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Điều kiện: tan x > 0
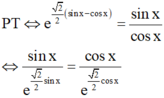
Xét hàm số y = f t = t e 2 2 t t ∈ - 1 ; 1
Khi đó f ' t = e 2 2 1 - t 2 2 e 2 t > 0 ∀ t ∈ - 1 ; 1
do đó hàm số f(t) đồng biến trên [–1;1]
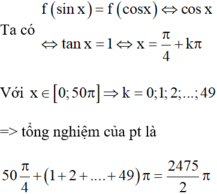


\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
Đáp án B
Điều kiện tan x > 0
PT ⇔ e 2 2 sin x - cos x = sin x cos x ⇔ sin x e 2 2 sin x = cos x e 2 2 cos x
Xét hàm số y = f t = t e 2 2 t t - 1 ; 1
Khi đó f ' t = e 2 2 t 1 - t 2 2 e 2 t > 0 ∀ t - 1 ; 1 do đó hàm số f(t) đồng biến trên [-1;1]
Ta có f sin x = f cos x ⇔ cos x ⇔ tan x = 1 ⇔ x = π 4 + k π
Với x ∈ 0 ; 50 π ⇒ k = 0 ; 1 ; 2 ; . . . ; 49 ⇒ tổng nghiệm của pt là
50 π 4 + 1 + 2 + . . . + 49 π = 2475 2 π