Phương trình sau có bao nhiêu nghiệm:
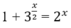
A. 0 B. 1
C. 2 D. Vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có \(\left|x\right|\ge0\) nên |x| + 1 > 0 với mọi x. Do đó phương trình đã cho vô nghiệm.
b) Tương tự, phân tích \(x^2+2x+3=\left(x+1\right)^2+2>0\)

D.\(x^2+5x+9< 0\)
\(x^2+5x+9=\left(x^2+2x.\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right)-\left(\dfrac{5}{2}\right)^2+9=\left(x+\dfrac{5}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}>0\)
Mà \(x^2+5x+9< 0\)
--> pt vô nghiệm

Chọn B và D
Phương trình B vô nghiệm vì \(5x^2+10\ge10>0\forall x\)
Phương trình C vô nghiệm vì \(x^2+6\ge6>-9\forall x\)
B và C
vì \(5x^2+10=0\Leftrightarrow5x^2=-10\Leftrightarrow x^2=-2\)(VL)
\(x^2+6=-9\Leftrightarrow x^2=-15\left(VL\right)\)

\(\left(2x-2\right)\left(3x+6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
-> chọn C

\(a,\Leftrightarrow\Delta'=1-\left(m-5\right)\ge0\\ \Leftrightarrow6-m\ge0\Leftrightarrow m\le6\\ b,\Leftrightarrow\Delta'=m^2-\left(m^2-2m+5\right)\ge0\\ \Leftrightarrow2m-5\ge0\Leftrightarrow m\ge\dfrac{5}{2}\)
a. x2 + 2x + m - 5 =0
b2 - 4ac = 2 bình - 4. 1 . (m - 5 ) = 0
4 - 4m + 20 = 0
-4m + 24 =0
suy ra m = - 6
câu cx y như vậy :))))

Chọn D.
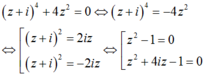
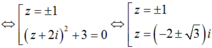
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đáp án : B.