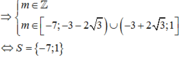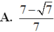Biết S = (a,b) là tập hợp tất cả các giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = | \(x^2-4x+3\) | tại bốn điểm phân biệt . Tìm a + b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 1 2020
Chọn D.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
Ta khảo sát hàm số (C): y = -x3 + 3x có đồ thị sau như hình bên.
Tìm được 
nên yêu cầu bài toán
CM
6 tháng 10 2019
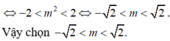
Đáp án B
Phương trình hoành độ giao điểm của (C) và (d) là x 3 − 3 x 2 = m ⇔ x 3 − 3 x 2 − m = 0 *
Để (C) cắt d tại 3 điểm phân biệt khi và chỉ khi (*) có 3 nghiệm phân biệt ⇔ − 4 < m < 0
Khi đó, gọi A x 1 ; m , B x 2 ; m , C x 3 ; m là giao điểm của (C) và d ⇒ A B ¯ = x 2 − x 1 ; 0 B C ¯ = x 3 − x 2 ; 0
Mà B nằm giữa A, C và A B = 2 B C suy ra A B ¯ = 2 B C ¯ ⇔ x 2 − x 1 = 2 x 3 − x 2 ⇔ x 1 + 2 x 3 = 3 x 2
Theo hệ thức Viet cho phương trình (*), ta được x 1 + x 2 + x 3 = 3 ; x 1 x 2 x 3 = m x 1 x 2 + x 2 x 3 + x 3 x 1 = 0
Giải x 1 − 3 x 2 + 2 x 3 = 0 x 1 + x 2 + x 3 = 3 x 1 x 2 + x 2 x 3 + x 3 x 1 = 0 ⇒ x 1 ; x 2 ; x 3 = 1 − 5 7 ; 1 + 1 7 ; 1 + 4 7 x 1 ; x 2 ; x 3 = 1 + 5 7 ; 1 − 1 7 ; 1 − 4 7 ⇒ m = − 98 + 20 7 49 m = − 98 − 20 7 49 ⇒ ∑ m = − 4
CM
7 tháng 7 2017
Đáp án C
Số giao điểm của đường thẳng y = ( m - 1 ) x và đồ thị hàm số y = x 3 - 3 x 2 + m + 1 là số nghiệm của PT x 3 - 3 x 2 + m + 1 = ( m - 1 ) x ⇔ x 3 - 3 x 2 + x + 1 - m x + m = 0 ⇔ ( x - 1 ) ( x 2 - 2 x - m - 1 ) = 0 để tồn tại ba giao điểm phân biệt thì 1 - 2 - m - 1 ≢ 0 ∆ ' = 1 + m + 1 > 0 ⇔ m ≢ - 2 m > - 2 khi đó tọa độ ba giao điểm là B ( 1 ; m - 1 ) , A ( x 1 ; y 1 ) , C ( x 2 ; y 2 ) hơn nữa x 1 + x 2 2 = 1 y 1 + y 2 2 = ( m - 1 ) x 1 + ( m - 1 ) x 2 2 = ( m - 1 ) ( x 1 + x 2 ) 2 = m - 1
⇒ B là trung điểm AC hay ta có AB=BC